
(1)过点P(0,0),Q(4,2),R(-1,-3)三点的圆的标准方程式什么?
(2)已知动点M到点A(2,0)的距离是它到点B(-1,0)的距离的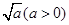 倍,求:(1)动点M的轨迹方程;(2)根据
倍,求:(1)动点M的轨迹方程;(2)根据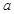 取值范围指出轨迹表示的图形.
取值范围指出轨迹表示的图形.
(1)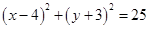 (2)见解析
(2)见解析
【解析】(1)先求出PQ和PR的垂直平分线方程,根据圆的几何性质可知圆心就是这两条垂直平分线的交点,然后根据两点间的距离公式求出半径,即可写出圆的标准方程.
(2)(i)设M(x,y),然后把这个条件动点M到点A(2,0)的距离是它到点B(-1,0)的距离的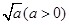 倍坐标化,再化简整理即可得取点M的轨迹方程.
倍坐标化,再化简整理即可得取点M的轨迹方程.
(ii)再根据a的取值范围根据方程来讨论轨迹形状.
解:(1)PQ中点为N(2,1) 
PR中点为M(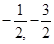 )
)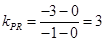
PQ中垂线的斜率为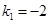 ,PQ中垂线所在直线方程
,PQ中垂线所在直线方程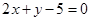
PR中垂线的斜率为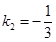 ,PR中垂线所在直线方程
,PR中垂线所在直线方程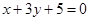
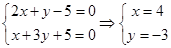 ,圆心(4,-3),r=5圆的标准方程
,圆心(4,-3),r=5圆的标准方程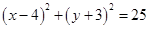
(2)设点M的坐标为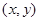

当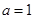 时,直线
时,直线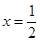
当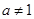 时,
时,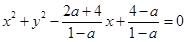
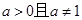 时,表示圆
时,表示圆
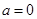 时,表示点(2,0)
时,表示点(2,0)
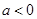 时,不表示任何图形
时,不表示任何图形


科目:高中数学 来源: 题型:
| PC |
| PQ |
| PC |
| PQ |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
A.3x2+![]() y2=1(x>0,y>0) B.3x2
y2=1(x>0,y>0) B.3x2![]() y2=1(x>0,y>0)
y2=1(x>0,y>0)
C.![]() x2-3y2=1(x>0,y>0) D.
x2-3y2=1(x>0,y>0) D.![]() x2+3y2=1(x>0,y>0)
x2+3y2=1(x>0,y>0)
查看答案和解析>>
科目:高中数学 来源: 题型:
A.3条 B.4条 C.1条 D.2条
查看答案和解析>>
科目:高中数学 来源:2011-2012学年重庆市高三上学期第十四次测试理科数学试卷(解析版) 题型:解答题
已知圆C: .
.
(1)直线 过点P(1,2),且与圆C交于A、B两点,若
过点P(1,2),且与圆C交于A、B两点,若 ,求直线
,求直线 的方程;
的方程;
(2)过圆C上一动点M作平行于y轴的直线m,设直线m与x轴的交点为N,若向量 ,求动点
,求动点 的轨迹方程;
的轨迹方程;
(3) 若点R(1,0),在(2)的条件下,求 的最小值及相应的
的最小值及相应的 点坐标.
点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com