
【题目】在平面直角坐标系![]() 中,
中,![]() 经过原点的直线
经过原点的直线![]() 将
将![]() 分成左、右两部分,记左、右两部分的面积分别为
分成左、右两部分,记左、右两部分的面积分别为![]() ,则
,则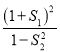 取得最小值时,直线
取得最小值时,直线![]() 的斜率( )
的斜率( )
A.等于1B.等于![]() C.等于
C.等于![]() D.不存在
D.不存在
【答案】D
【解析】
方法一:根据四个选项可知,分别计算![]() ,
,![]() ,
,![]() ,和
,和![]() 不存在时
不存在时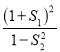 的值,比较大小即可;
的值,比较大小即可;
方法二:讨论斜率![]() ,
,![]() ,
,![]() 不存在三种情况,在三种情况下分别求出
不存在三种情况,在三种情况下分别求出![]() ,代入表达式
,代入表达式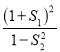 ,化简比较大小即可.
,化简比较大小即可.
方法一:因为,![]()
所以![]()
当![]() 时,
时,![]() ,此时
,此时![]() ,
,![]() ,∴
,∴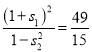
当![]() 时,
时, ![]() ,此时,
,此时,![]() ,
,![]() ,∴
,∴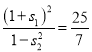
当![]() 时,
时, ![]() ,此时,
,此时, ![]() ,
,![]() ,∴
,∴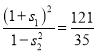
当![]() 不存在时,
不存在时, ![]() ,此时,
,此时, ![]() ,∴
,∴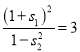
综上比较可知,当![]() 不存在时,
不存在时, 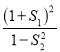 的值最小
的值最小
故选:D
方法二: 因为,![]()
所以![]()
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]()
直线![]() 的方程为
的方程为![]()
此时直线与![]() 相交,设交点为E,则
相交,设交点为E,则![]()
解方程可得E点坐标为![]()
则![]()
所以![]()
则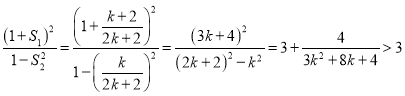
当![]() 时, 直线
时, 直线![]() 的方程为
的方程为![]()
直线![]() 的方程为
的方程为![]()
此时直线与![]() 相交,设交点为F,则
相交,设交点为F,则![]()
解方程可得F点坐标为![]()
则![]()
所以![]()
则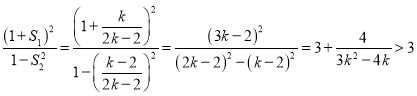
当![]() 不存在时
不存在时![]() ,此时,
,此时, ![]() ,∴
,∴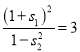
综上可知, 当![]() 不存在时,
不存在时, 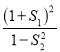 的值最小
的值最小
故选:D


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】如图所示的“8”字形曲线是由两个关于x轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是x2+y2﹣4y﹣4=0,双曲线的左、右顶点A、B是该圆与x轴的交点,双曲线与半圆相交于与x轴平行的直径的两端点.
(1)试求双曲线的标准方程;
(2)记双曲线的左、右焦点为F1、F2,试在“8”字形曲线上求点P,使得∠F1PF2是直角.
(3)过点A作直线l分别交“8”字形曲线中上、下两个半圆于点M、N,求|MN|的最大长度.
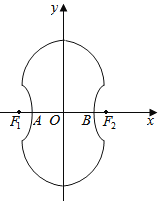
查看答案和解析>>
科目:高中数学 来源: 题型:
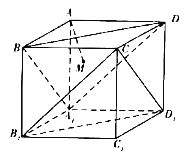
【题目】如图,在正方体ABCD﹣A1B1C1D1中,AM⊥平面A1BD,垂足为M,以下四个结论中正确的个数为( )
①AM垂直于平面CB1D1;
②直线AM与BB1所成的角为45°;
③AM的延长线过点C1;
④直线AM与平面A1B1C1D1所成的角为60°
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】8个女孩和25个男孩围成一圈,任何两个女孩之间至少站两个男孩,则共有__________________种不同的排列方法.(只要把圈旋转一下就重合的排法认为是相同的).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,马路![]() 南边有一小池塘,池塘岸
南边有一小池塘,池塘岸![]() 长40米,池塘的最远端
长40米,池塘的最远端![]() 到
到![]() 的距离为400米,且池塘的边界为抛物线型,现要在池塘的周边建一个等腰梯形的环池塘小路
的距离为400米,且池塘的边界为抛物线型,现要在池塘的周边建一个等腰梯形的环池塘小路![]() ,且
,且![]() 均与小池塘岸线相切,记
均与小池塘岸线相切,记![]() .
.

(1)求小路的总长,用![]() 表示;
表示;
(2)若在小路与小池塘之间(图中阴影区域)铺上草坪,求所需铺草坪面积最小时,![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是______.
①若直线![]() 与直线
与直线![]() 互相垂直,则
互相垂直,则![]()
②若![]() ,
,![]() 两点到直线
两点到直线![]() 的距离分别是
的距离分别是![]() ,
,![]() ,则满足条件的直线
,则满足条件的直线![]() 共有3条
共有3条
③过![]() ,
,![]() 两点的所有直线方程可表示为
两点的所有直线方程可表示为![]()
④经过点![]() 且在
且在![]() 轴和
轴和![]() 轴上截距都相等的直线方程为
轴上截距都相等的直线方程为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是______.
①若直线![]() 与直线
与直线![]() 互相垂直,则
互相垂直,则![]()
②若![]() ,
,![]() 两点到直线
两点到直线![]() 的距离分别是
的距离分别是![]() ,
,![]() ,则满足条件的直线
,则满足条件的直线![]() 共有3条
共有3条
③过![]() ,
,![]() 两点的所有直线方程可表示为
两点的所有直线方程可表示为![]()
④经过点![]() 且在
且在![]() 轴和
轴和![]() 轴上截距都相等的直线方程为
轴上截距都相等的直线方程为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两点![]() 、
、![]() ,动点
,动点![]() 满足
满足![]() ,记
,记![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() (
(![]() )交曲线
)交曲线![]() 于
于![]() 、
、![]() 两点,点
两点,点![]() 在第一象限,
在第一象限,![]() 轴,垂足为
轴,垂足为![]() ,连结
,连结![]() 并延长交曲线
并延长交曲线![]() 于点
于点![]() .
.
(1)求曲线![]() 的方程,并说明曲线
的方程,并说明曲线![]() 是什么曲线;
是什么曲线;
(2)若![]() ,求△
,求△![]() 的面积;
的面积;
(3)证明:△![]() 为直角三角形.
为直角三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一片森林原面积为![]() ,计划从某年开始,每年砍伐一些树林,且每年砍伐面积与上一年剩余面积的百分比相等.并计划砍伐到原面积的一半时,所用时间是10年.为保护生态环境,森林面积至少要保留原面积的
,计划从某年开始,每年砍伐一些树林,且每年砍伐面积与上一年剩余面积的百分比相等.并计划砍伐到原面积的一半时,所用时间是10年.为保护生态环境,森林面积至少要保留原面积的![]() .已知到今年为止,森林剩余面积为原面积的
.已知到今年为止,森林剩余面积为原面积的![]() .
.
(1)求每年砍伐面积与上一年剩余面积的百分比;
(2)到今年为止,该森林已砍伐了多少年?
(3)为保护生态环境,今后最多还能砍伐多少年?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com