

图1-3-15
(1)求证:△ABC∽△FCD;
(2)若S△FCD?=5,BC=10,求DE的长.
思路分析:第(1)问,∵AD = AC,∴∠ACB=∠CDF.又D是BC中点,ED⊥BC,?
∴∠B=∠ECD.∴△ABC∽△FCD.?
第(2)问利用相似三角形的性质,作AM⊥BC于M,易知S△ABC=4S△FCD.∴S△ABC=20,AM =4.
又∵AM∥ED,∴![]() =
=![]() .再根据等腰三角形的性质及中点,可以求出DE.也可运用△ABC∽△FCD,由相似比为2,证出F是AD的中点,通过“两三角形等底等高,则面积相等”,求出S△ABC=20.
.再根据等腰三角形的性质及中点,可以求出DE.也可运用△ABC∽△FCD,由相似比为2,证出F是AD的中点,通过“两三角形等底等高,则面积相等”,求出S△ABC=20.

(1)证明:∵DE⊥BC,D是BC中点,∴EB =EC.?
∴∠B=∠1.?
又∵AD=AC,∴∠2=∠ACB.?
∴△ABC∽△FCD.
(2)解法一:过点A作AM⊥BC,垂足为点M.(如图所示)?
∵△ABC∽△FCD,BC =2CD,?
∴![]() =(
=(![]() )2=4.?
)2=4.?
又∵S△FCD =5,∴S△ABC =20.?
∵S△ABC?=![]() BC·AM,BC =10,
BC·AM,BC =10,
∴20 =![]() ×10×AM.∴AM =4.?
×10×AM.∴AM =4.?
又∵DE∥AM,∴![]() =
=![]() .?
.?
∵![]()
![]() ,BM =BD +DM,BD =
,BM =BD +DM,BD =![]() ,∴
,∴![]() =
=![]() .?
.?
∴![]() .?
.?
解法二:作FH⊥BC,垂足为点H.(如图所示)?
∵S△FCD =![]() DC·FH,?
DC·FH,?
又∵S△FCD?=5, ![]() ,?
,?
∴5=![]() ×5×FH.∴FH =2.?
×5×FH.∴FH =2.?
过点A作AM⊥BC,垂足为点M,?
∵△ABC∽△FCD,?
∴![]() =
=![]() =
=![]() .∴AM =4.?
.∴AM =4.?
又∵FH∥AM,∴![]() =
=![]() =
=![]() =
=![]() .?
.?
∴点H是DM的中点.?
又∵FH∥DE,∴![]() =
=![]() .?
.?
∵HC =HM +MC=![]() ,∴
,∴![]() =
=![]() .∴
.∴![]() .
.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
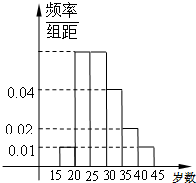 某单位组织群众性登山健身活动,招募了N名师生志愿者,将所有志愿者现按年龄情况分为15-20,20-25,25-30,30-35,35-40,40-45等六个层次,其频率分布直方图如图所示:已知30-35之间的志愿者共8人.
某单位组织群众性登山健身活动,招募了N名师生志愿者,将所有志愿者现按年龄情况分为15-20,20-25,25-30,30-35,35-40,40-45等六个层次,其频率分布直方图如图所示:已知30-35之间的志愿者共8人.查看答案和解析>>
科目:高中数学 来源: 题型:

图
(1)求证:AE与⊙O相切于点A.
(2)当AB不是直径时,其他条件不变,结论还成立吗?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图1-2(3)-15,某炮兵阵地位于A点,两观察所分别位于C、D两点.已知△ACD为正三角形,且DC=

查看答案和解析>>
科目:高中数学 来源: 题型:
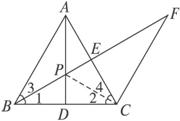
图1-3-15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com