
分析 分别求出满足P,q成立的x的范围,求出p∧q的范围,根据集合的包含关系得到关于a的不等式组,解出即可.
解答 解:由题可知,命题p:-1<x<3,
命题q:2<x<4,…..(2分)
故p∧q:2<x<3.…(4分)
根据a>0,及p∧q是r的充分条件可知:$\left\{\begin{array}{l}a≤2\\ 3≤2a\end{array}\right.$;…(8分)
解得 $\frac{3}{2}≤a≤2$,
综上可知,a的取值范围是$\left\{{\left.a\right|}\right.\frac{3}{2}≤a≤2\left.{\;}\right\}$.…(10分)
点评 本题考查了充分必要条件,考查复合命题的判断,是一道基础题.


科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
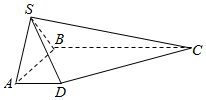 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AB垂直于AD和BC,平面SAB⊥底面ABCD,且SA=SB=$\sqrt{2}$,AD=1,AB=2,BC=3.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AB垂直于AD和BC,平面SAB⊥底面ABCD,且SA=SB=$\sqrt{2}$,AD=1,AB=2,BC=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
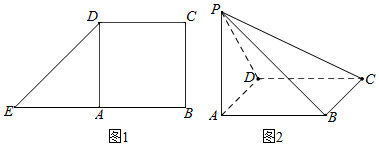
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
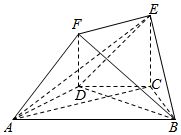 如图,已知直角梯形ACEF与等腰梯形ABCD所在的平面互相垂直,EF∥AC,EF═$\frac{1}{2}$AC,EC⊥AC,AD=DC=CB=CE=$\frac{1}{2}$AB=1.
如图,已知直角梯形ACEF与等腰梯形ABCD所在的平面互相垂直,EF∥AC,EF═$\frac{1}{2}$AC,EC⊥AC,AD=DC=CB=CE=$\frac{1}{2}$AB=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -tanθ | B. | tanθ | C. | -cosθ | D. | sinθ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | (?p)∧q | C. | p∧(?q) | D. | (?p)∧(?q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
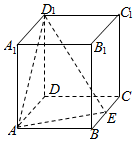 如图,正方体ABCD-A1B1C1D1中,E是棱BC的中点,F是侧面BCC1B1上的动点,且A1F∥平面AD1E,则直线A1F与平面BCC1B1所成的角的正切值t构成的集合是( )
如图,正方体ABCD-A1B1C1D1中,E是棱BC的中点,F是侧面BCC1B1上的动点,且A1F∥平面AD1E,则直线A1F与平面BCC1B1所成的角的正切值t构成的集合是( )| A. | {t|${\frac{{2\sqrt{5}}}{5}$≤t≤$\frac{{2\sqrt{3}}}{3}}\right.}$} | B. | {t|{2≤t≤2$\sqrt{3}}$} | C. | {t|${\frac{{2\sqrt{5}}}{5}$≤t≤2$\sqrt{3}$} | D. | {{t|{2≤t≤2$\sqrt{2}}$} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com