解:(方法一)设所求的圆的方程是(x-a)
2+(y-b)
2=r
2,
则圆心(a,b)到直线x-y=0的距离为
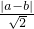
,∴
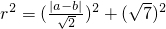
即2r
2=(a-b)
2+14①(2分)
由于所求的圆与x轴相切,∴r
2=b
2②(4分)
又圆心在直线3x-y=0上,∴3a-b=0③(6分)
联立①②③,解得a=1,b=3,r
2=9或a=-1,b=3,r
2=9(10分)
故所求的圆的方程是:(x-1)
2+(y-3)
2=9或(x+1)
2+(y+3)
2=9(12分)
(方法二)设所求的圆的方程是x
2+y
2+Dx+Ey+F=0,则其圆心为
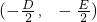
,
半径为
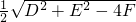
,令y=0得x
2+Dx+F=0,由圆与x轴相切,
得△=0,即D
2=4F④(2分)
又圆心
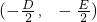
到直线x-y=0的距离为
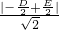
,由已知得
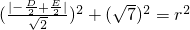
,
即(D-E)
2+56=2(D
2+E
2-4F)⑤(4分)
又圆心
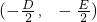
在直线3x-y=0上,∴3D-E=0⑥(6分)
联立④⑤⑥,解得:D=-1,E=-6,F=1或D=2,E=6,F=1(10分)
故所求圆的方程是x
2+y
2-2x-6y+1=0或x
2+y
2+2x+6y+1=0(12分)
(方法三)由题,设所求圆的圆心为(3t,t),则其半径r=3|t|(4分)
方程为(x-t)
2+(y-3t)
2=9t
2,圆心到直线x-y=0的距离为
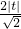
(6分)
∴
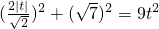
,解得t=1或t=-1(10分)
故所求的圆的方程是:(x-1)
2+(y-3)
2=9或(x+1)
2+(y+3)
2=9(12分)
分析:法一:设出圆的方程,利用已知条件,推出2r
2=(a-b)
2+14①,r
2=b
2②,3a-b=0③解出a,b,r即可得到圆的方程.
法二:设出圆的一般方程,利用圆锥条件,求出D、E、F即可得到圆的方程.
法三:设所求圆的圆心为(t,3t),则其半径r=3|t|,方程为(x-t)
2+(y-3t)
2=9t
2,圆心到直线x-y=0的距离为
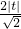
,求出t,解出圆的方程.
点评:本题是基础题,考查圆的方程的求法,标准方程与一般方程的应用,灵活设出圆的圆心坐标与半径,简化解题过程是最好的解题方法,考查计算能力.

 ,求圆C的方程.
,求圆C的方程.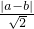 ,∴
,∴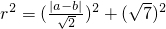
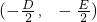 ,
,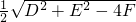 ,令y=0得x2+Dx+F=0,由圆与x轴相切,
,令y=0得x2+Dx+F=0,由圆与x轴相切,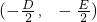 到直线x-y=0的距离为
到直线x-y=0的距离为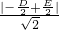 ,由已知得
,由已知得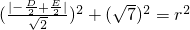 ,
,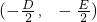 在直线3x-y=0上,∴3D-E=0⑥(6分)
在直线3x-y=0上,∴3D-E=0⑥(6分)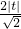 (6分)
(6分)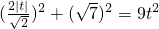 ,解得t=1或t=-1(10分)
,解得t=1或t=-1(10分)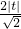 ,求出t,解出圆的方程.
,求出t,解出圆的方程.
