
 ”中,△、Θ都为正整数,且它们的倒数之和最小,则△、Θ的值分别为
”中,△、Θ都为正整数,且它们的倒数之和最小,则△、Θ的值分别为 +a(x>0)的形式,利用基本不等式求最值,则由取最值的条件即可解决问题.
+a(x>0)的形式,利用基本不等式求最值,则由取最值的条件即可解决问题. ”有:
”有: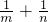 =
=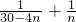 =
= ,
,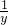 =
= =
= =
=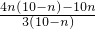 =
=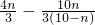 =
=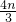 +
+
 =
= -
-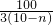 +
+ =-
=- [(10-n)+
[(10-n)+ ]+
]+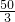 ≤-
≤- ×2×
×2×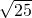 +
+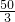 =
= .
. 时取等号,即
时取等号,即 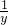 取得最大值,y取得最小值.
取得最大值,y取得最小值. +a(x>0,a为常数)的代数式的转化方法,注意分子次数必须高于分母次数;同时考查基本不等式的运用条件,特别是取等号时的条件.该题代数运较为繁琐,运算量较大,属于难题.
+a(x>0,a为常数)的代数式的转化方法,注意分子次数必须高于分母次数;同时考查基本不等式的运用条件,特别是取等号时的条件.该题代数运较为繁琐,运算量较大,属于难题. 

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 4 |
| △ |
| 1 |
| Θ |
| 30 |
| △×Θ |
| A、6,6 | B、10,5 |
| C、14,4 | D、18,3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com