
【题目】某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为120件,80件,60件.为了解它们的产品质量是否存在显著差异,用分层抽样方法抽取了一个容量为n的样本进行调查,其中从丙车间的产品中抽取了3件,则n=( )
A.9
B.10
C.12
D.13
科目:高中数学 来源: 题型:
【题目】在以下关于向量的命题中,不正确的是( )
A.若向量 ![]() ,向量
,向量 ![]() (xy≠0),则
(xy≠0),则 ![]()
B.若四边形ABCD为菱形,则 ![]()
C.点G是△ABC的重心,则 ![]()
D.△ABC中, ![]() 和
和 ![]() 的夹角等于A
的夹角等于A
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中, ![]() 平面PCD,平面PAD平面ABCD,CD⊥AD,△APD为等腰直角三角形,
平面PCD,平面PAD平面ABCD,CD⊥AD,△APD为等腰直角三角形, ![]() .
. 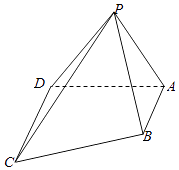
(1)证明:平面PAB⊥平面PCD;
(2)若三棱锥B﹣PAD的体积为 ![]() ,求平面PAD与平面PBC所成二面角的余弦值.
,求平面PAD与平面PBC所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(m,cos2x),
=(m,cos2x), ![]() =(sin2x,n),设函数f(x)=
=(sin2x,n),设函数f(x)= ![]()
![]() ,且y=f(x)的图象过点(
,且y=f(x)的图象过点( ![]() ,
, ![]() )和点(
)和点( ![]() ,﹣2).
,﹣2).
(1)求m,n的值;
(2)将y=f(x)的图象向左平移φ(0<φ<π)个单位后得到函数y=g(x)的图象.若y=g(x)的图象上各最高点到点(0,3)的距离的最小值为1,求y=g(x)的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了解学生数学课程的学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测,这3000名学生在该次数学考试中成绩小于60分的学生数是 . 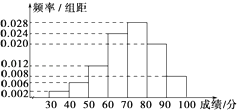
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计算下列几个式子,结果为 ![]() 的序号是 . ①tan25°+tan35°
的序号是 . ①tan25°+tan35° ![]() tan25°tan35°,
tan25°tan35°,
② ![]() ,
,
③2(sin35°cos25°+sin55°cos65°),
④ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,其中a>0,a≠1.
,其中a>0,a≠1.
(Ⅰ)若f(x)在(﹣∞,+∞)上是单调函数,求实数a,b的取值范围;
(Ⅱ)当a=2时,函数f(x)在(﹣∞,+∞)上只有一个零点,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,BC⊥DC , AE⊥DC , M , N分别是AD , BE的中点,将三角形ADE沿AE折起,则下列说法正确的是(填序号).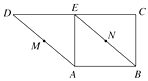
①不论D折至何位置(不在平面ABC内),都有MN∥平面DEC;②不论D折至何位置,都有MN⊥AE;③不论D折至何位置(不在平面ABC内),都有MN∥AB;④在折起过程中,一定存在某个位置,使EC⊥AD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com