
【题目】已知数列{an}的各项均为非零实数,且对于任意的正整数n,都有(a1+a2+a3+…+an)2=a13+a23+a33+…+an3 .
(1)写出数列{an}的前三项a1 , a2 , a3(请写出所有可能的结果);
(2)是否存在满足条件的无穷数列{an},使得a2017=﹣2016?若存在,求出这样的无穷数列的一个通项公式;若不存在,说明理由;
(3)记an点所有取值构成的集合为An , 求集合An中所有元素之和(结论不要证明).
【答案】
(1)解:当n=1时,a13=a12,由a1≠0得a1=1.
当n=2时,1+a23=(1+a2)2,由a2≠0得a2=2或a2=﹣1.
当n=3时,1+a23+a33=(1+a2+a3)2,若a2=2得a3=3或a3=﹣2;若a2=﹣1得a3=1;
综上讨论,满足条件的数列有三个:1,2,3或1,2,﹣2或1,﹣1,1
(2)解:令Sn=a1+a2+…+an,则Sn2=a13+a23+…+an3(n∈N*).
从而(Sn+an+1)2=a13+a23+…+an3+an+13,
两式相减,结合an+1≠0,得2Sn=an+12﹣an+1.
当n=1时,由(1)知a1=1;
当n≥2时,2an=2(Sn﹣Sn﹣1)=(an+12﹣an+1)﹣(an2﹣an),即(an+1+an)(an+1﹣an﹣1)=0,
所以an+1=﹣an或an+1=an+1.
又a1=1,a2017=﹣2016,所以无穷数列{an}的前2016项组成首项和公差均为1的等差数列,从第2016项开始组成首项为﹣2016,公比为﹣1的等比数列.
an= ![]()
(3)解:由(2)可知a1=1,an=﹣an﹣1或an=an﹣1+1(n≥2),
故A1={1},A2={﹣1,2},A3={1,﹣2,3},A4={﹣1,2,﹣3,4},…
∴当n为奇数时,An的所有元素之和为1+3+5+…+n﹣(2+4+6+…n﹣1)= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
当n为偶数时,An的所有元素之和为2+4+6+…+n﹣(1+3+5+…+n﹣1)= ![]() ﹣
﹣ ![]() =
= ![]()
【解析】(1)利用数列递推式,n分别取1,2,3,代入计算,即可得到结论;(2)令Sn=a1+a2+…+an,Sn2=a13+a23+…+an3(n∈N*).可得再写一式,两式相减,可得数列{an}的任一项an与它的前一项an﹣1间的递推关系;利用a1=1,a2017=﹣2016,所以无穷数列{an}的前2016项组成首项和公差均为1的等差数列,从第2016项开始组成首项为﹣2016,公比为﹣1的等比数列,从而可得数列的通项.(3)根据递推式得出An的所有元素规律,利用归纳法得出结论.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,PC⊥平面ABCD,点E在棱PA上. 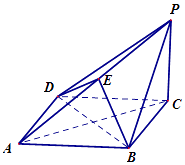
(Ⅰ)求证:直线BD⊥平面PAC;
(Ⅱ)若PC∥平面BDE,求证:AE=EP;
(Ⅲ)是否存在点E,使得四面体A﹣BDE的体积等于四面体P﹣BDC的体积的 ![]() ?若存在,求出
?若存在,求出 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要想得到函数 ![]() 的图象,只需将函数y=sinx的图象上所有的点( )
的图象,只需将函数y=sinx的图象上所有的点( )
A.先向右平移 ![]() 个单位长度,再将横坐标伸长为原来的2倍,纵坐标不变
个单位长度,再将横坐标伸长为原来的2倍,纵坐标不变
B.先向右平移 ![]() 个单位长度,横坐标缩短为原来的
个单位长度,横坐标缩短为原来的 ![]() 倍,纵坐标不变
倍,纵坐标不变
C.横坐标缩短为原来的 ![]() 倍,纵坐标不变,再向右平移
倍,纵坐标不变,再向右平移 ![]() 个单位长度
个单位长度
D.横坐标变伸长原来的2倍,纵坐标不变,再向右平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的公比q=2,前3项和是7,等差数列{bn}满足b1=3,2b2=a2+a4 . (Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)求数列 ![]() 的前n项和Sn .
的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx﹣ ![]() )(ω>0)的图象与x轴的相邻两个交点的距离为
)(ω>0)的图象与x轴的相邻两个交点的距离为 ![]() .
.
(1)求w的值;
(2)设函数g(x)=f(x)+2cos2x﹣1,求g(x)在区间 ![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥P﹣ABC的各顶点都在同一球的面上,且PA⊥平面ABC,若球O的体积为 ![]() (球的体积公式为
(球的体积公式为 ![]() R3 , 其中R为球的半径),AB=2,AC=1,∠BAC=60°,则三棱锥P﹣ABC的体积为( )
R3 , 其中R为球的半径),AB=2,AC=1,∠BAC=60°,则三棱锥P﹣ABC的体积为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,AB= ![]() ,AF=1,G为线段AD上的任意一点.
,AF=1,G为线段AD上的任意一点. 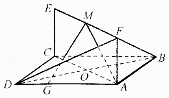
(1)若M是线段EF的中点,证明:平面AMG⊥平面BDF;
(2)若N为线段EF上任意一点,设直线AN与平面ABF,平面BDF所成角分别是α,β,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]()
![]() ,其中
,其中 ![]() =(2cosx,﹣
=(2cosx,﹣ ![]() sin2x),
sin2x), ![]() =(cosx,1),x∈R.
=(cosx,1),x∈R.
(1)求f(x)的单调递减区间;
(2)在△ABC中,角A,B,C所对的边分别为a,b,c,f(A)=﹣1,a= ![]() ,且向量
,且向量 ![]() =(3,sinB)与
=(3,sinB)与 ![]() =(2,sinC)共线,求边长b和c的值.
=(2,sinC)共线,求边长b和c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() )x , 函数g(x)=log
)x , 函数g(x)=log ![]() x.
x.
(1)若g(ax2+2x+1)的定义域为R,求实数a的取值范围;
(2)当x∈[( ![]() )t+1 , (
)t+1 , ( ![]() )t]时,求函数y=[g(x)]2﹣2g(x)+2的最小值h(t);
)t]时,求函数y=[g(x)]2﹣2g(x)+2的最小值h(t);
(3)是否存在非负实数m,n,使得函数y=log ![]() f(x2)的定义域为[m,n],值域为[2m,2n],若存在,求出m,n的值;若不存在,则说明理由.
f(x2)的定义域为[m,n],值域为[2m,2n],若存在,求出m,n的值;若不存在,则说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com