
【题目】已知函数![]() .
.
(1)判断函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)讨论函数![]() 的零点的个数.
的零点的个数.
【答案】(1)当![]() 时,函数
时,函数![]() 为偶函数;当
为偶函数;当![]() 时,函数
时,函数![]() 为非奇非偶函数;详见解析(2)当
为非奇非偶函数;详见解析(2)当![]() 时,函数
时,函数![]() 有2个零点;当
有2个零点;当![]() 时,函数
时,函数![]() 有1个零点
有1个零点
【解析】
(1)根据奇偶函数的定义判断可得;
(2)将函数![]() 化为分段函数后,对
化为分段函数后,对![]() 分五种情况讨论可求得函数的零点.
分五种情况讨论可求得函数的零点.
(1) 当![]() 时,函数
时,函数![]() 为偶函数;当
为偶函数;当![]() 时,函数
时,函数![]() 为非奇非偶函数,
为非奇非偶函数,
理由如下:
当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() 为偶函数;
为偶函数;
当![]() 时,
时,![]() 不恒等于0,所以
不恒等于0,所以![]() 不为奇函数,
不为奇函数,
![]() 不恒等于0,所以
不恒等于0,所以![]() 不为偶函数,
不为偶函数,
所以![]() 为非奇非偶函数.
为非奇非偶函数.
(2)因为![]() ,
,
①当![]() 时,当
时,当![]() 时,由
时,由![]() ,可得
,可得![]() ,
,
当![]() 时, 由
时, 由![]() 得
得![]() (舍去),
(舍去),
所以函数![]() 有唯一零点,
有唯一零点,
②当![]() 时,
时, ![]() ,
,
所以函数![]() 有唯一零点
有唯一零点![]() ,
,
③当![]() 时, 当
时, 当![]() 时,由
时,由![]() ,可得
,可得![]() ,
,
当![]() 时, 由
时, 由![]() 得
得![]() ,
,
所以函数![]() 有两个零点,
有两个零点,
④当![]() 时,函数
时,函数![]() ,
,
所以函数![]() 有唯一零点
有唯一零点![]() ,
,
⑤当![]() 时, 当
时, 当![]() 时,由
时,由![]() ,可得
,可得![]() (舍去),
(舍去),
当![]() 时, 由
时, 由![]() 得
得![]() ,
,
所以函数![]() 有唯一零点,
有唯一零点,
综上所述: 当![]() 时,函数
时,函数![]() 有2个零点;当
有2个零点;当![]() 时,函数
时,函数![]() 有1个零点.
有1个零点.


科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的左右顶点分别为
的左右顶点分别为![]() .直线
.直线![]() 和两条渐近线交于点
和两条渐近线交于点![]() ,点
,点![]() 在第一象限且
在第一象限且![]() ,
,![]() 是双曲线上的任意一点.
是双曲线上的任意一点.
(1)求双曲线的标准方程;
(2)是否存在点P使得![]() 为直角三角形?若存在,求出点P的个数;
为直角三角形?若存在,求出点P的个数;
(3)直线![]() 与直线
与直线![]() 分别交于点
分别交于点![]() ,证明:以
,证明:以![]() 为直径的圆必过定点.
为直径的圆必过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为更好地落实农民工工资保证金制度,南方某市劳动保障部门调查了2018年下半年该市![]() 名农民工(其中技术工、非技术工各
名农民工(其中技术工、非技术工各![]() 名)的月工资,得到这
名)的月工资,得到这![]() 名农民工的月工资均在
名农民工的月工资均在![]() (百元)内,且月工资收入在
(百元)内,且月工资收入在![]() (百元)内的人数为
(百元)内的人数为![]() ,并根据调查结果画出如图所示的频率分布直方图:
,并根据调查结果画出如图所示的频率分布直方图:
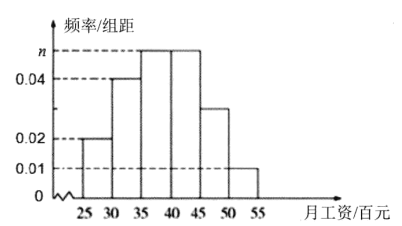
(1)求![]() 的值;
的值;
(2)已知这![]() 名农民工中月工资高于平均数的技术工有
名农民工中月工资高于平均数的技术工有![]() 名,非技术工有
名,非技术工有![]() 名.
名.
①完成如下所示![]() 列联表
列联表
技术工 | 非技术工 | 总计 | |
月工资不高于平均数 |
| ||
月工资高于平均数 |
| ||
总计 |
|
|
|
②则能否在犯错误的概率不超过![]() 的前提下认为是不是技术工与月工资是否高于平均数有关系?
的前提下认为是不是技术工与月工资是否高于平均数有关系?
参考公式及数据: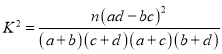 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
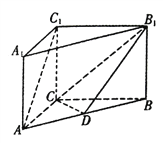
【题目】直三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 是线段
是线段![]() 上的动点.
上的动点.
(1)当点![]() 是
是![]() 的中点时,求证:
的中点时,求证: ![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,试求出
?若存在,试求出![]() 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,对任意的
,对任意的![]() ,都有
,都有![]() .
.
(1)求数列![]() 的递推公式
的递推公式
(2)数列![]() 满足
满足![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)在(2)的条件下,设![]() ,问是否存在实数
,问是否存在实数![]() 使得数列
使得数列![]() 是单调递增数列?若存在,求出
是单调递增数列?若存在,求出![]() 的取值范围;若不存在,请说明你的理由.
的取值范围;若不存在,请说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种病毒感染性腹泻在全世界范围内均有流行,感染对象主要是成人和学龄儿童,寒冷季节呈现高发,据资料统计,某市11月1日开始出现该病毒感染者,11月1日该市的病毒新感染者共有20人,此后每天的新感染者比前一天的新感染者增加50人,由于该市医疗部分采取措施,使该病毒的传播速度得到控制,从第![]() 天起,每天的新感染者比前一天的新感染者减少30人,直到11月30日为止.
天起,每天的新感染者比前一天的新感染者减少30人,直到11月30日为止.
(1)设11月![]() 日当天新感染人数为
日当天新感染人数为![]() ,求
,求![]() 的通项公式(用
的通项公式(用![]() 表示);
表示);
(2)若到11月30日止,该市在这30日感染该病毒的患者共有8670人,11月几日,该市感染此病毒的新患者人数最多?并求出这一天的新患者人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的各项都是正数,且对于任意
的各项都是正数,且对于任意![]() 都有
都有![]() ,记
,记![]() 为数列
为数列![]() 的前
的前![]() 项和.
项和.
(1)计算![]() 的值;
的值;
(2)求数列![]() 的通项公式;
的通项公式;
(3)设![]() ,若
,若![]() 为单调递增数列,求
为单调递增数列,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内两个定点![]() 和点
和点![]() ,
,![]() 是动点,且直线
是动点,且直线![]() ,
,![]() 的斜率乘积为常数
的斜率乘积为常数![]() ,设点
,设点![]() 的轨迹为
的轨迹为![]() .
.
① 存在常数![]() ,使
,使![]() 上所有点到两点
上所有点到两点![]() 距离之和为定值;
距离之和为定值;
② 存在常数![]() ,使
,使![]() 上所有点到两点
上所有点到两点![]() 距离之和为定值;
距离之和为定值;
③ 不存在常数![]() ,使
,使![]() 上所有点到两点
上所有点到两点![]() 距离差的绝对值为定值;
距离差的绝对值为定值;
④ 不存在常数![]() ,使
,使![]() 上所有点到两点
上所有点到两点![]() 距离差的绝对值为定值.
距离差的绝对值为定值.
其中正确的命题是_______________.(填出所有正确命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com