
【题目】已知抛物线C: ![]() ,点
,点 ![]() 在x轴的正半轴上,过点M的直线
在x轴的正半轴上,过点M的直线 ![]() 与抛物线C相交于A,B两点,O为坐标原点.
与抛物线C相交于A,B两点,O为坐标原点.
(1)若 ![]() ,且直线
,且直线 ![]() 的斜率为1,求以AB为直径的圆的方程;
的斜率为1,求以AB为直径的圆的方程;
(2)是否存在定点M,使得不论直线 ![]() 绕点M如何转动,
绕点M如何转动, ![]() 恒为定值?
恒为定值?
【答案】
(1)解:当 ![]() 时,
时, ![]() ,此时,点M为抛物线C的焦点,
,此时,点M为抛物线C的焦点,
直线 ![]() 的方程为
的方程为 ![]() ,设
,设 ![]() ,联立
,联立 ![]() ,
,
消去y得, ![]() ,∴
,∴ ![]() ,
, ![]() ,∴圆心坐标为
,∴圆心坐标为 ![]() .
.
又 ![]() ,∴圆的半径为4,∴圆的方程为
,∴圆的半径为4,∴圆的方程为 ![]()
(2)解:由题意可设直线 ![]() 的方程为
的方程为 ![]() ,则直线
,则直线 ![]() 的方程与抛物线C:
的方程与抛物线C: ![]() 联立,
联立,
消去x得: ![]() ,则
,则 ![]() ,
, ![]() ,
,![]()
![]() 对任意
对任意 ![]() 恒为定值,
恒为定值,
于是 ![]() ,此时
,此时 ![]() .
.
∴存在定点 ![]() ,满足题意
,满足题意
【解析】(1)根据条件可求出直线l的方程,将直线方程与抛物线方程联立后,利用韦达定理可得出以A、B为直径的圆的半径、圆心坐标,写出圆的方程即可。
(2)根据条件设出直线l的方程,与抛物线方程联立后表示出A、B坐标,代入给出的式子、化简后得到![]() =
=![]() ,则
,则![]() 即k=2试该式恒为定值。
即k=2试该式恒为定值。


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】每年的4月23日为世界读书日,为调查某高校学生(学生很多)的读书情况,随机抽取了男生,女生各20人组成的一个样本,对他们的年阅读量(单位:本)进行了统计,分析得到了男生年阅读量的频率分布表和女生阅读量的频率分布直方图. 男生年阅读量的频率分布表(年阅读量均在区间[0,60]内):
本/年 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60] |
频数 | 3 | 1 | 8 | 4 | 2 | 2 |
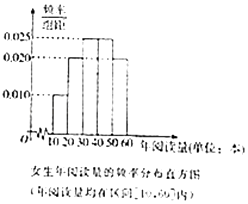
(1)根据女生的频率分布直方图估计该校女生年阅读量的中位数;
(2)在样本中,利用分层抽样的方法,从男生年与度量在[20,30),[30,40)的两组里抽取6人,再从这6人中随机抽取2人,求[30,40)这一组中至少有1人被抽中的概率;
(3)若年阅读量不小于40本为阅读丰富,否则为阅读不丰富,依据上述样本研究阅读丰富与性别的关系,完成下列2×2列联表,并判断是否有99%的把握认为月底丰富与性别有关.
性别 阅读量 | 丰富 | 不丰富 | 合计 |
男 | |||
女 | |||
合计 |
P(K2≥k0) | 0.025 | 0.010 | 0.005 |
k0 | 5.024 | 6.635 | 7.879 |
附:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系中,曲线C1的参数方程为 ![]() (φ为参数),以原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ.
(φ为参数),以原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ.
(Ⅰ)求曲线C1的极坐标方程与曲线C2的直角坐标方程;
(Ⅱ)若直线θ= ![]() (ρ∈R)与曲线C1交于P,Q两点,求|PQ|的长度.
(ρ∈R)与曲线C1交于P,Q两点,求|PQ|的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题错误的是( )
A.命题“若 ![]() ,则
,则 ![]() ”的逆命题为“若
”的逆命题为“若 ![]() ,则
,则 ![]() ”
”
B.对于命题 ![]() ,使得
,使得 ![]() ,则
,则 ![]() ,则
,则 ![]()
C.“ ![]() ”是“
”是“ ![]() ”的充分不必要条件
”的充分不必要条件
D.若 ![]() 为假命题,则
为假命题,则 ![]() 均为假命题
均为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《算法统综》是明朝程大位所著数学名著,其中有这样一段表述:“远看巍巍塔七层,红光点点倍加增,共灯三百八十一”,其意大致为:有一七层宝塔,每层悬挂的红灯数为上一层的两倍,共有381盏灯,则塔从上至下的第三层有( )盏灯.
A.14
B.12
C.10
D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市电视台为了提高收视率而举办有奖问答活动,随机对该市15~65岁的人群抽样了 ![]() 人,回答问题统计结果及频率分布直方图如图表所示.
人,回答问题统计结果及频率分布直方图如图表所示.
(1)分别求出 ![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组至少有1人获得幸运奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,已知圆
中,已知圆 ![]() ,点
,点 ![]() ,点
,点 ![]() ,以B为圆心,
,以B为圆心, ![]() 为半径作圆,交圆C于点P,且
为半径作圆,交圆C于点P,且 ![]() 的平分线交线段CP于点Q.
的平分线交线段CP于点Q.
(1)当a变化时,点Q始终在某圆锥曲线 ![]() 上运动,求曲线
上运动,求曲线 ![]() 的方程;
的方程;
(2)已知直线l过点C,且与曲线 ![]() 交于M,N两点,记
交于M,N两点,记 ![]() 面积为
面积为 ![]() ,
, ![]() 面积为
面积为 ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从参加某次高中英语竞赛的学生中抽出100名,将其成绩整理后,绘制频率分布直方图(如图所示).其中样本数据分组区间为: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
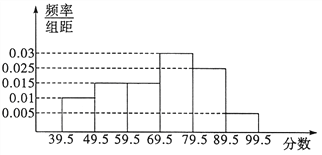
(Ⅰ)试求图中![]() 的值,并计算区间
的值,并计算区间![]() 上的样本数据的频率和频数;
上的样本数据的频率和频数;
(Ⅱ)试估计这次英语竞赛成绩的众数、中位数及平均成绩(结果精确到![]() ).
).
注:同一组数据用该组区间的中点值作为代表
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com