
【题目】若函数f(x)=(1﹣x2)(x2+ax+b)的图象关于直线x=﹣2对称,则f(x)的最大值为 .
【答案】16
【解析】解:∵函数f(x)=(1﹣x2)(x2+ax+b)的图象关于直线x=﹣2对称,
∴f(﹣1)=f(﹣3)=0且f(1)=f(﹣5)=0,
即[1﹣(﹣3)2][(﹣3)2+a(﹣3)+b]=0且[1﹣(﹣5)2][(﹣5)2+a(﹣5)+b]=0,
解之得 ![]() ,
,
因此,f(x)=(1﹣x2)(x2+8x+15)=﹣x4﹣8x3﹣14x2+8x+15,
求导数,得f′(x)=﹣4x3﹣24x2﹣28x+8,
令f′(x)=0,得x1=﹣2﹣ ![]() ,x2=﹣2,x3=﹣2+
,x2=﹣2,x3=﹣2+ ![]() ,
,
当x∈(﹣∞,﹣2﹣ ![]() )时,f′(x)>0;当x∈(﹣2﹣
)时,f′(x)>0;当x∈(﹣2﹣ ![]() ,﹣2)时,f′(x)<0;
,﹣2)时,f′(x)<0;
当x∈(﹣2,﹣2+ ![]() )时,f′(x)>0; 当x∈(﹣2+
)时,f′(x)>0; 当x∈(﹣2+ ![]() ,+∞)时,f′(x)<0
,+∞)时,f′(x)<0
∴f(x)在区间(﹣∞,﹣2﹣ ![]() )、(﹣2,﹣2+
)、(﹣2,﹣2+ ![]() )上是增函数,在区间(﹣2﹣
)上是增函数,在区间(﹣2﹣ ![]() ,﹣2)、(﹣2+
,﹣2)、(﹣2+ ![]() ,+∞)上是减函数.
,+∞)上是减函数.
又∵f(﹣2﹣ ![]() )=f(﹣2+
)=f(﹣2+ ![]() )=16,
)=16,
∴f(x)的最大值为16.
所以答案是:16.
【考点精析】本题主要考查了函数的最大(小)值与导数的相关知识点,需要掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
【题目】正项数列{an}的前n项和Sn满足:Sn2 ![]()
(1)求数列{an}的通项公式an;
(2)令b ![]() ,数列{bn}的前n项和为Tn . 证明:对于任意n∈N* , 都有
,数列{bn}的前n项和为Tn . 证明:对于任意n∈N* , 都有 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,CA=CB,AB=AA1 , ∠BAA1=60°. 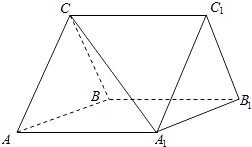
(1)证明AB⊥A1C;
(2)若平面ABC⊥平面AA1B1B,AB=CB,求直线A1C与平面BB1C1C所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(选修4﹣5:不等式选讲)
已知函数f(x)=|2x﹣1|+|2x+a|,g(x)=x+3.
(1)当a=﹣2时,求不等式f(x)<g(x)的解集;
(2)设a>﹣1,且当 ![]() 时,f(x)≤g(x),求a的取值范围.
时,f(x)≤g(x),求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四张卡片,分别写有“瓷、都、文、明”四个字,有放回地从中任取一张卡片,将三次抽取后“瓷”“都”两个字都取到记为事件![]() ,用随机模拟的方法估计事件
,用随机模拟的方法估计事件![]() 发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
232 | 321 | 230 | 023 | 123 | 021 | 132 | 220 | 001 |
231 | 130 | 133 | 231 | 031 | 320 | 122 | 103 | 233 |
由此可以估计事件![]() 发生的概率为( )
发生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com