
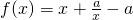 ,
,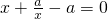 有正根?方程x2-ax+a=0有正根.△=a2-4a
有正根?方程x2-ax+a=0有正根.△=a2-4a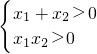 成立,所以a>4符合题意∵a<0时,使得x1x2<0成立,所以a<0符合题意.
成立,所以a>4符合题意∵a<0时,使得x1x2<0成立,所以a<0符合题意.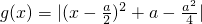
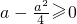 即0≤a≤4时,g(x)在区间
即0≤a≤4时,g(x)在区间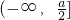 上是减函数,又已知g(x)在区间[0,1]上是减函数,
上是减函数,又已知g(x)在区间[0,1]上是减函数, 即a≥2,
即a≥2,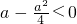 即a>4或a<0时,设方程g(x)=0的两根为x1,x2且x1<x2,此时g(x)
即a>4或a<0时,设方程g(x)=0的两根为x1,x2且x1<x2,此时g(x)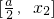 上是减函数,若[0,1]?(-∞,x1],则
上是减函数,若[0,1]?(-∞,x1],则 得a>2
得a>2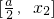 ,则
,则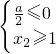
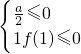 此时a不存在
此时a不存在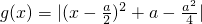 ,根据g(x)的图象特征,分
,根据g(x)的图象特征,分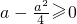 和
和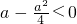 时进行讨论,即可求得结果.
时进行讨论,即可求得结果.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 给出下列四个命题:
给出下列四个命题:| π |
| 6 |
| 5 |
| 6 |
| OA |
| OB |
| OC |
| ||
|
| 1 |
| 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010-2011学年安徽省六安一中高三(下)第七次月考数学试卷(理科)(解析版) 题型:填空题
 ;
; ,则α+β=1是A、B、C三点共线的充要条件;
,则α+β=1是A、B、C三点共线的充要条件; (p为正常数,n∈N*),则称数列an是“等方比数列”.根据此定义可以断定:若数列an是“等方比数列”,则它一定是等比数列;
(p为正常数,n∈N*),则称数列an是“等方比数列”.根据此定义可以断定:若数列an是“等方比数列”,则它一定是等比数列;

查看答案和解析>>
科目:高中数学 来源:河北省模拟题 题型:解答题
 是否有实数解.
是否有实数解.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com