
����Ŀ��ij�о���ѧϰС�����ҹ�²��С��ij���ӷ�ѿ����֮��Ĺ�ϵ�����о���������3��1����5��ÿ����ҹ�²���ʵ����ÿ��ÿ100�����ӽ��ݺ�ķ�ѿ������ϸ��¼��
(1)����3��2����3��4�յ����ݣ�����С���˷����y����x�����Իع鷽�̣�
���� | 3��1�� | 3��2�� | 3��3�� | 3��4�� | 3��5�� |
�²� | 10 | 11 | 13 | 12 | 8 |
��ѿ�� | 23 | 25 | 30 | 26 | 16 |
(2)�������Իع鷽�̵õ��Ĺ�����������ѡ���ļ������ݵ�����С��2�ţ�����Ϊ�õ������Իع鷽���ǿɿ��ģ�����(1)�����õ����Իع鷽���Ƿ�ɿ���
�ο���ʽ�� ��
��![]() ��
��
���𰸡�(1) ![]() (2)������
(2)������
��������
��1��������²�x�ͷ�ѿ��y��ƽ��ֵ�����õ��������ĵ㣬������С���˷��õ����Իع鷽�̵�ϵ���������������ĵ������Իع�ֱ���ϣ��õ�aֵ���������Իع鷽�̣���2���ֱ���֤��x��10��x��8ʱ��yֵ����֤|y��23|��2��|y��16|��2�ɵý���.
��1�������ݣ����![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ���ɹ�ʽ�����
���ɹ�ʽ�����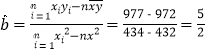 ��
��
![]() ��
��
����y����x�����Իع鷽��Ϊ![]() ��
��
��2����x��10ʱ��![]() ��|22��23|��2��
��|22��23|��2��
ͬ������x��8ʱ��![]() ��|17��16|��2��
��|17��16|��2��
���ԣ����о����õ������Իع鷽���ǿɿ��ģ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������![]() �У�
��![]() ��
��![]() ���е㣬
���е㣬![]() ���߶�
���߶�![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() .
.
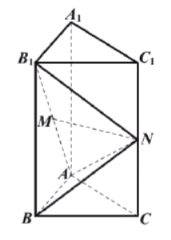
��1����![]() ����֤��
����֤��![]() ��
��
��2��������![]() ������ֵ��
������ֵ��
��3����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵĴ�СΪ
���ɽǵĴ�СΪ![]() ����
����![]() �����ֵ
�����ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() ��
�� ![]() ��
�� ![]() .
.
��1������![]() �ĵ����ԣ�
�ĵ����ԣ�
��2����![]() ʱ������
ʱ������![]() ��ͼ���ϴ��ڵ��ں���
��ͼ���ϴ��ڵ��ں���![]() ��ͼ����·�����
��ͼ����·�����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڸ�����������![]() ��������
��������![]() ����
����![]() ������������
������������![]() �ܳ������������
�ܳ������������![]() �ǡ�
�ǡ�![]() ���С�.
����.
(1)֤�����Ȳ�����![]() �ǡ�
�ǡ�![]() ���С���
������
(2)������![]() ���ǡ�
���ǡ�![]() ���С������ǡ�
���С������ǡ�![]() ���С���֤����
���С���֤���� ![]() �ǵȲ�����.
�ǵȲ�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڼ�����ϵ�У�����C���ѣ�2sin�ȣ�A��BΪ����C�����㣬�Լ���Ϊԭ�㣬����Ϊx��Ǹ������ֱ�������У�����E��![]() �Dz���)��һ��P�����APB�����ֵΪ (�� ��)
�Dz���)��һ��P�����APB�����ֵΪ (�� ��)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�������ƽ��չ��ͼ,�����ı���![]() Ϊ������,
Ϊ������,![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ���е�.�ڴ˼�������,�������н���,������ȷ�Ľ�����( )
���е�.�ڴ˼�������,�������н���,������ȷ�Ľ�����( )
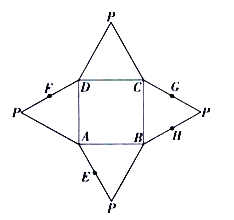
A.ƽ��![]() ƽ��
ƽ��![]() B.ֱ��
B.ֱ��![]() ƽ��
ƽ��![]()
C.ֱ��![]() ƽ��
ƽ��![]() D.ֱ��
D.ֱ��![]() ƽ��
ƽ��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������12������֪������![]() ��������
��������![]() �Ǿ�������
�Ǿ�������![]() ��
��![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() �ֱ����߶�
�ֱ����߶�![]() ��
��![]() ���е�.
���е�.
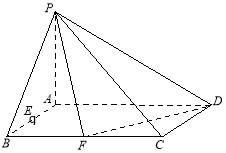
��1���жϲ�˵��![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() ƽ��
ƽ��![]() ?�����ڣ����
?�����ڣ����![]() ��ֵ������
��ֵ������
���ڣ���˵��������
��2����![]() ��ƽ��
��ƽ��![]() ���ɵĽ�Ϊ
���ɵĽ�Ϊ![]() ��������
��������![]() ��ƽ��ǵ�����ֵ.
��ƽ��ǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ϊ�˻�ø�������棬ÿ��ҪͶ��һ�����ʽ����ڹ�������������Ͷ�����t(����Ԫ)�����������۶�ԼΪ��t2��5t(����Ԫ)(0��t��5) (ע�����棽���۶Ͷ��)��
��1�����ù�˾������Ĺ��ѿ�����3����Ԫ֮�ڣ���ӦͶ����ٹ��ѣ�����ʹ�ù�˾�ɴ˻�õ��������
��2���ָù�˾����Ͷ��3����Ԫ���ֱ����ڹ������ͼ������죮��Ԥ�⣬ÿͶ�뼼�������x(����Ԫ)�������ӵ����۶�ԼΪ��![]() x3��x2��3x(����Ԫ)�������һ���ʽ���䷽����ʹ�ù�˾�ɴ˻�õ��������
x3��x2��3x(����Ԫ)�������һ���ʽ���䷽����ʹ�ù�˾�ɴ˻�õ��������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com