
【题目】已知关于![]() 不等式
不等式![]() 的解集为
的解集为![]() .
.
(1)当![]() 为空集时,求
为空集时,求![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,求![]() 的最小值;
的最小值;
(3)当![]() 不为空集,且
不为空集,且![]() 时,求实数
时,求实数![]() 的取值范围.
的取值范围.
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
【题目】以下有四个说法:
①若![]() 、
、![]() 为互斥事件,则
为互斥事件,则![]() ;
;
②在![]() 中,
中,![]() ,则
,则![]() ;
;
③![]() 和
和![]() 的最大公约数是
的最大公约数是![]() ;
;
④周长为![]() 的扇形,其面积的最大值为
的扇形,其面积的最大值为![]() ;
;
其中说法正确的个数是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市调研考试后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的![]() 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为![]() .
.
优秀 | 非优秀 | 合计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 110 |
(1)请完成上面的列联表;
(2)根据列联表的数据,若按99%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到9号或10号的概率.
参考公式及数据:![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定直线l:y=x+3,定点A(2,1),以坐标轴为对称轴的椭圆C过点A且与l相切. 
(Ⅰ)求椭圆的标准方程;
(Ⅱ)椭圆的弦AP,AQ的中点分别为M,N,若MN平行于l,则OM,ON斜率之和是否为定值?若是定值,请求出该定值;若不是定值请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面命题正确的是( )
A.“![]() ”是“
”是“![]() ”的 充 分不 必 要条件
”的 充 分不 必 要条件
B.命题“若![]() ,则
,则![]() ”的 否 定 是“ 存 在
”的 否 定 是“ 存 在![]() ,则
,则![]() ”.
”.
C.设![]() ,则“
,则“![]() 且
且![]() ”是“
”是“![]() ”的必要而不充分条件
”的必要而不充分条件
D.设![]() ,则“
,则“![]() ”是“
”是“![]() ”的必要 不 充 分 条件
”的必要 不 充 分 条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数集A由实数构成:且满足:若![]() ,则
,则![]()
(1)若![]() ,试证明A中还有另外两个元素;
,试证明A中还有另外两个元素;
(2)集合A是否为双元素集合,并说明理由;
(3)若集合A是有限集,求集合A中所有元素的积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,并且b=2
(1)若角A,B,C成等差数列,求△ABC外接圆的半径;
(2)若三边a,b,c成等差数列,求△ABC内切圆半径的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱台ABCD﹣A1B1C1D1中,底面ABCD为平行四边形,∠BAD=120°,M为CD上的点.且∠A1AB=∠A1AD=90°,AD=A1A=2,A1B1=DM=1. 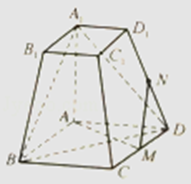
(1)求证:AM⊥A1B;
(2)若M为CD的中点,N为棱DD1上的点,且MN与平面A1BD所成角的正弦值为 ![]() ,试求DN的长.
,试求DN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com