
【题目】已知a>0且a≠1,函数f(x)= ![]() (a﹣x﹣ax),g(x)=﹣ax+2.
(a﹣x﹣ax),g(x)=﹣ax+2.
(1)指出f(x)的单调性(不要求证明);
(2)若有g(2)+f(2)=3,求g(﹣2)+f(﹣2)的值;
(3)若h(x)=f(x)+g(x)﹣2,求使不等式h(x2+tx)+h(4﹣x)<0恒成立的t的取值范围.
【答案】
(1)解:由题意:函数f(x)= ![]() (a﹣x﹣ax),
(a﹣x﹣ax),
①当0<a<1时, ![]() 递减,
递减,
②当a>1时, ![]() 递减,
递减,
∴当且a>0且a≠1时,f(x)是减函数
(2)解:由题意g(x)=﹣ax+2.
设h(x)=f(x)+g(x)﹣2,则:h(x)= ![]() ,其定义域为R,关于原点对称,
,其定义域为R,关于原点对称,
h(﹣x)= ![]() =
= ![]() =﹣[
=﹣[ ![]() ]=﹣h(x)
]=﹣h(x)
∵h(﹣x)=﹣h(x),
∴h(x)是定义域为R的奇函数.
∵g(2)+f(2)=3,则:h(2)=1,
∴h(﹣2)=﹣1,即:g(2)+f(2)﹣2=﹣1
所以g(2)+f(2)=1
(3)解:由(2)知h(x)是定义域为R的奇函数,且在R上为减函数,
由h(x2+tx)+h(4﹣x)<0,则有:h(x2+tx)<h(﹣4+x)
∴x2+tx>x﹣4,即x2+(t﹣1)x+4>0 恒成立,
∴△=b2﹣4ac=(t﹣1)2﹣16<0
解得:﹣3<t<5,
故得t的取值范围是(﹣3,5)
【解析】(1)利用指数函数的单调性,对底数a讨论,即可单调性.(2)令f(x)+g(x)﹣2=h(x).证明其奇偶性,利用奇偶性求值.(3)利用(1)(2)中的结论,将不等式转化为二次函数恒成立问题,即可求解t的取值范围.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】过点![]() 作一直线与抛物线
作一直线与抛物线![]() 交于
交于![]() 两点,点
两点,点![]() 是抛物线
是抛物线![]() 上到直线
上到直线![]() :
: ![]() 的距离最小的点,直线
的距离最小的点,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
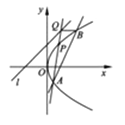
(Ⅰ)求点![]() 的坐标;
的坐标;
(Ⅱ)求证:直线![]() 平行于抛物线的对称轴.
平行于抛物线的对称轴.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知![]() ,在直角坐标系
,在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数);在以坐标原点
为参数);在以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,直线
轴的正半轴为极轴的极坐标系中,直线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)设点![]() 的极坐标为
的极坐标为![]() ,
, ![]() 为直线
为直线![]() ,
, ![]() 的交点,求
的交点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中,PA垂直于底面ABC,∠ACB=90°,AE⊥PB于E,AF⊥PC于F,若PA=AB=2,∠BPC=θ,则当△AEF的面积最大时,tanθ的值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知离心率为 ![]() 的椭圆
的椭圆 ![]() 过点M(2,1),O为坐标原点,平行于OM的直线i交椭圆C于不同的两点A、B.
过点M(2,1),O为坐标原点,平行于OM的直线i交椭圆C于不同的两点A、B. 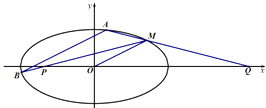
(1)求椭圆C的方程;
(2)记直线MB、MA与x轴的交点分别为P、Q,若MP斜率为k1 , MQ斜率为k2 , 求k1+k2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若二次函数f(x)=ax2+bx+c(a,b,c∈R)满足f(x+1)﹣f(x)=4x+1,且f(0)=3.
(1)求f(x)的解析式;
(2)设g(x)=f(2x),求g(x)在[﹣3,0]的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C与x轴相切,圆心C在射线3x﹣y=0(x>0)上,直线x﹣y=0被圆C截得的弦长为2 ![]()
(1)求圆C标准方程;
(2)若点Q在直线l1:x+y+1=0上,经过点Q直线l2与圆C相切于p点,求|QP|的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com