
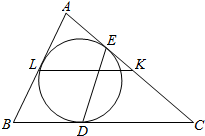
 如图,己知L、K分别是△ABC的边AB、AC的中点.△ABC的内切圆⊙l分别与边BC、CA切于点D、E.求证:KL、DE的交点在∠ABC的角平分线上.
如图,己知L、K分别是△ABC的边AB、AC的中点.△ABC的内切圆⊙l分别与边BC、CA切于点D、E.求证:KL、DE的交点在∠ABC的角平分线上. 分析 设KL与∠ABC的角平分线交于点S,DE与∠ABC的角平分线交于点T,进而证明出S,T重合,利用同一法,可得KL、DE的交点在∠ABC的角平分线上.
解答 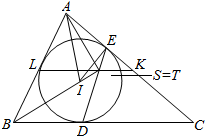 证明:如图所示:设KL与∠ABC的角平分线交于点S,
证明:如图所示:设KL与∠ABC的角平分线交于点S,
∵L、K分别是△ABC的边AB、AC的中点.
∴LK∥BC,
∴∠LSB=∠CBS=∠LBS,
∴LB=LS,
又∵LA=LS,
∴S在以AB为直径的圆上,
∴∠ASB=90°,
设DE与∠ABC的角平分线交于点T,
则△ABC的内心I在点B,T之间,
当AB≠BC时,T≠E,且∠DEC=90°-$\frac{1}{2}$∠C,∠AIB=90°+$\frac{1}{2}$∠C,
如果T在线面DE内部,有∠AIT+∠AET=180°,
∴A,I,T,E四点共圆,
如果I和E在AT的同侧,则有∠AIT=90°,$\frac{1}{2}$∠C=∠AET,
也有A,I,T,E四点共圆,
∵∠AEI=90°,
∴∠AIT=90°,
∵∠ASB=∠ATB,
则S和T重合,
即KL、DE的交点在∠ABC的角平分线上.
点评 本题考查的知识点是圆的切线的性质定理,同一法证明,圆内接四边形的判定与性质,难度较大.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 8 | ||
| C. | 4 | D. | 不确定,与k值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
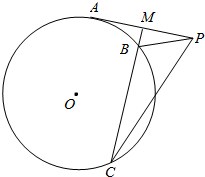 自⊙O外一点p引切线与⊙O切于点A,M为PA的中点,过M引割线交⊙O于B、C两点.
自⊙O外一点p引切线与⊙O切于点A,M为PA的中点,过M引割线交⊙O于B、C两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
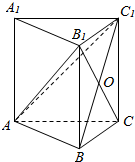 如图,三棱柱ABC-A1B1C1中,AC⊥BC,侧棱C1C⊥平面ABC,AC=BC=CC1=2,B1C与BC1相交于点O,连结AB1,AC1.
如图,三棱柱ABC-A1B1C1中,AC⊥BC,侧棱C1C⊥平面ABC,AC=BC=CC1=2,B1C与BC1相交于点O,连结AB1,AC1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
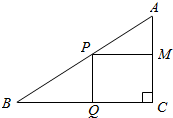 直角三角形ABC的直角顶点为C,且AC=3cm,BC=4cm,P为斜边AB上一点,PQ平行于AC且交BC于点Q,PM平行于BC且交AC于点M,问点P在边AB何处时,矩形PQCM的面积最大?最大面积是多少?
直角三角形ABC的直角顶点为C,且AC=3cm,BC=4cm,P为斜边AB上一点,PQ平行于AC且交BC于点Q,PM平行于BC且交AC于点M,问点P在边AB何处时,矩形PQCM的面积最大?最大面积是多少?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com