
(本题满分12分)有甲、乙两种商品,经营销售这两种商品所能获得的利润依次是P和Q(万元),它们与投入资金x(万元)的关系有经验公式:P= x,Q=
x,Q=
 .今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少,能获得的最大利润为多少?
.今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少,能获得的最大利润为多少?
为了获得最大利润,对甲、乙两种商品的资金投入应分别为0.75万元和2.25万元,获得最高利润1.05万元.
【解析】本题考查了二次根式在实际问题中的运用.关键是根据题意列方程,两边平方去根号转化为关于x的一元二次方程,利用判别式求解.
根据3万元资金投入经营甲、乙两种商品,设投入甲x万元,则投入乙(3-x)万元,根据总利润=甲的利润+乙的利润,列方程并平方整理为关于x的一元二次方程,由△≥0,求s的最大值,并求出此时x的值.
解:设对甲种商品投资x万元,获总利润为y万元,则对乙种商品的投资为(3-x)万元,于是y= x+
x+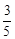
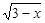 (0≤x≤3).
(0≤x≤3).
令t=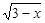 (0≤t≤
(0≤t≤ ),则x=3-t2,
),则x=3-t2,
∴y= (3-t2)+
(3-t2)+
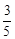 t=
t= (3+3t-t2)
=-
(3+3t-t2)
=- (t-
(t-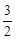 )2+
)2+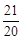 ,t∈[0,
,t∈[0, ].
].
∴当t=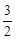 时,ymax=
时,ymax=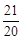 =1.05(万元); 由t=
=1.05(万元); 由t=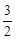 可求得x=0.75(万元), 3-x=2.25(万元),
可求得x=0.75(万元), 3-x=2.25(万元),
∴为了获得最大利润,对甲、乙两种商品的资金投入应分别为0.75万元和2.25万元,获得最高利润1.05万元.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
(本题满分12分)有混在一起质地均匀且粗细相同的长分别为1![]() 、2
、2![]() 、3
、3![]() 的钢管各3根(每根钢管附有不同的编号),现随意抽取4根(假设各钢管被抽取的可能性是均等的),再将抽取的4根首尾相接焊成笔直的一根.
的钢管各3根(每根钢管附有不同的编号),现随意抽取4根(假设各钢管被抽取的可能性是均等的),再将抽取的4根首尾相接焊成笔直的一根.
(1)若用ξ表示新焊成的钢管的长度(焊接误差不计),试求随机变量![]() 的分布列及
的分布列及![]() ;
;
(2)设![]() 的取值从小到大依次为
的取值从小到大依次为![]() 数列
数列![]() 是首项为1,公差为
是首项为1,公差为![]() 的等差数列,设
的等差数列,设![]() ,当
,当![]() 时,求
时,求![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2014届云南省高一上学期期中数学试卷(解析版) 题型:解答题
(本题满分12分)有甲、乙两种商品,经销这两种商品所能获得的利润分别是 万元和
万元和 万元,它们与投入资金万元的关系为:
万元,它们与投入资金万元的关系为: 今有3万元资金投入经营这两种商品,为获得最大利润,对这两种商品的资金分别投入多少时,能获得最大利润?最大利润是多少?
今有3万元资金投入经营这两种商品,为获得最大利润,对这两种商品的资金分别投入多少时,能获得最大利润?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源:山东省09-10高一下学期数学期末试题 题型:解答题
(本题满分12分) 袋中有大小、形状相同的红、黑球各一个,现依次有放回地随机摸取
3次,每次摸取一个球.
(I) 试问;一共有多少种不同的结果? 请列出所有可能的结果;
(II) 若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率.
查看答案和解析>>
科目:高中数学 来源:2013届云南省高二上学期期末考试理科数学 题型:解答题
(本题满分12分)有一枚正方体骰子,六个面分别写1、2、3、4、5、6的数字,规定“抛掷该枚骰子得到的数字是抛掷后,面向上的那一个数字”。已知b和c是先后抛掷该枚骰子得到的数字,函数 =
= 。
。
(Ⅰ)若先抛掷骰子得到的数字是3,求再次抛掷骰子时,使函数 有零点的概率;
有零点的概率;
(Ⅱ) 求函数 在区间(—3,+∞)是增函数的概率
在区间(—3,+∞)是增函数的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com