
【题目】为了调查某生产线上质量监督员甲对产品质量好坏有无影响,现统计数据如下:质量监督员甲在生产现场时,990件产品中合格品有982件,次品有8件;甲不在生产现场时,510件产品中合格品有493件,次品有17件,试分别用列联表、独立性检验的方法分析监督员甲是否在生产现场对产品质量好坏有无影响?
【答案】答案见解析
【解析】试题分析:
由题意写出列联表,然后由题意计算|ac-bd|=12 750,相差较大,可在某种程度上认为“质量监督员甲是否在生产现场与产品质量有关系”.
利用独立性检验的方法求得k≈13.097>6.635,
所以在犯错误的概率不超过0.01的前提下,认为质量监督员甲是否在生产现场与产品质量有关系.
试题解析:
(1)2×2列联表如下:
合格品数 | 次品数 | 总计 | |
甲在生产现场 | 982 | 8 | 990 |
甲不在生产现场 | 493 | 17 | 510 |
总计 | 1 475 | 25 | 1 500 |
由列联表可得|ac-bd|=|982×17-493×8|=12 750,相差较大,可在某种程度上认为“质量监督员甲是否在生产现场与产品质量有关系”.
(2)由2×2列联表中数据,计算得到K2的观测值为
k=![]() ≈13.097>6.635,
≈13.097>6.635,
所以在犯错误的概率不超过0.01的前提下,认为质量监督员甲是否在生产现场与产品质量有关系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某教师有相同的语文参考书3本,相同的数学参考书4本,从中取出4本赠送给4位学生,每位学生1本,则不同的赠送方法共有( )
A. 15种 B. 20种 C. 48种 D. 60种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料:
日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
(1)从3月1日至3月5日中任选2天,记发芽的种子数分别为![]() ,求事件“
,求事件“![]() 均小于25”的概率;
均小于25”的概率;
(2)请根据3月2日至3月4日的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)所得的线性回归方程是否可靠?
(参考公式:回归直线方程为![]() ,其中
,其中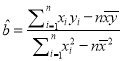 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)设![]() ,
, ![]() 是曲线
是曲线![]() 图象上的两个相异的点,若直线
图象上的两个相异的点,若直线![]() 的斜率
的斜率![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() 有两个极值点
有两个极值点![]() ,
, ![]() ,且
,且![]() ,若
,若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为实常数).
为实常数).
(1)若![]() ,
, ![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)若![]() ,且
,且![]() ,求函数
,求函数![]() 在
在![]() 上的最小值及相应的
上的最小值及相应的![]() 值;
值;
(3)设![]() ,若存在
,若存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着智能手机的发展,微信越来越成为人们交流的一种方式,某机构对使用微信交流的态度进行调查,随机调查了50人,他们年龄的频数分布及对使用微信交流赞成人数如表:
年龄(岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)由以上统计数据填写下面![]() 列联表,并判断是否有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;
列联表,并判断是否有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;
年龄不低于45岁的人 | 年龄低于45岁的人 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若对年龄分别在![]() ,
, ![]() 的被调查人中各抽取一人进行追踪调查,求选中的2人中至少有一人赞成使用微信交流的概率.
的被调查人中各抽取一人进行追踪调查,求选中的2人中至少有一人赞成使用微信交流的概率.
参考公式: ![]() ,其中
,其中![]()
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学餐饮中心为了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合 计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合 计 | 70 | 30 | 100 |
⑴根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差
异”;
⑵已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机
抽取3人,求至多有1人喜欢甜品的概率.
| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
附: 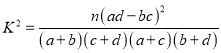 ,
,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com