
【题目】已知对任意平面向量 ![]() =(x,y),把
=(x,y),把 ![]() 绕其起点沿逆时针方向旋转θ角得到的向量
绕其起点沿逆时针方向旋转θ角得到的向量 ![]() =(xcosθ﹣ysinθ,xsinθ+ycosθ),叫做把点B绕点A逆时针方向旋转θ得到点P.
=(xcosθ﹣ysinθ,xsinθ+ycosθ),叫做把点B绕点A逆时针方向旋转θ得到点P.
(1)已知平面内点A(2,3),点B(2+2 ![]() ,1).把点B绕点A逆时针方向旋转
,1).把点B绕点A逆时针方向旋转 ![]() 角得到点P,求点P的坐标.
角得到点P,求点P的坐标.
(2)设平面内曲线C上的每一点绕坐标原点沿顺时针方向旋转 ![]() 后得到的点的轨迹方程是曲线y=
后得到的点的轨迹方程是曲线y= ![]() ,求原来曲线C的方程.
,求原来曲线C的方程.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设离心率为 ![]() 的椭圆
的椭圆![]() 的左、右焦点为
的左、右焦点为![]() , 点P是E上一点,
, 点P是E上一点, ![]() ,
, ![]() 内切圆的半径为
内切圆的半径为 ![]() .
.
(1)求E的方程;
(2)矩形ABCD的两顶点C、D在直线![]() 上,A、B在椭圆E上,若矩形ABCD的周长为
上,A、B在椭圆E上,若矩形ABCD的周长为 ![]() , 求直线AB的方程.
, 求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设Ox、Oy是平面内相交成45°角的两条数轴, ![]() 、
、 ![]() 分别是x轴、y轴正方向同向的单位向量,若向量
分别是x轴、y轴正方向同向的单位向量,若向量 ![]() =x
=x ![]() +y
+y ![]() ,则把有序数对(x,y)叫做向量
,则把有序数对(x,y)叫做向量 ![]() 在坐标系xOy中的坐标,在此坐标系下,假设
在坐标系xOy中的坐标,在此坐标系下,假设 ![]() =(﹣2,2
=(﹣2,2 ![]() ),
), ![]() =(2,0),
=(2,0), ![]() =(5,﹣3
=(5,﹣3 ![]() ),则下列命题不正确的是( )
),则下列命题不正确的是( ) 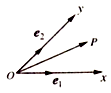
A.![]() =(1,0)
=(1,0)
B.| ![]() |=2
|=2 ![]()
C.![]() ∥
∥ ![]()
D.![]() ⊥
⊥ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
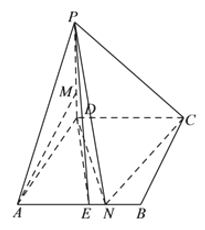
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 中点.
中点.
(I)求证:直线![]() 平面
平面![]() .
.
(II)求证:直线![]() 平面
平面![]() .
.
(III)在![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ,若存在,确定
,若存在,确定![]() 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若将函数y=cos 2x的图象向左平移 ![]() 个单位长度,则平移后图象的对称轴为( )
个单位长度,则平移后图象的对称轴为( )
A.x= ![]() ﹣
﹣ ![]() (k∈Z)
(k∈Z)
B.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
C.x= ![]() ﹣
﹣ ![]() (k∈Z)
(k∈Z)
D.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在(0, ![]() )上的函数f(x),f′(x)是它的导函数,且恒有f(x)<f′(x)tanx成立,则( )
)上的函数f(x),f′(x)是它的导函数,且恒有f(x)<f′(x)tanx成立,则( )
A.![]() f(
f( ![]() )>
)> ![]() f(
f( ![]() )
)![]()
B.f(1)<2f( ![]() )sin1
)sin1
C.![]() f(
f( ![]() )>f(
)>f( ![]() )
)![]()
D.![]() f(
f( ![]() )<f(
)<f( ![]() )
)![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
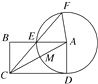
【题目】如图,在矩形ABCD中,以A为圆心,AD为半径的圆交AC,AB于M,E.CE的延长线交⊙A于F,CM=2,AB=4.
(1)求⊙A的半径;
(2)求CE的长和△AFC的面积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在实常数![]() 和
和![]() ,使得函数
,使得函数![]() 和
和![]() 对其定义域上的任意实数
对其定义域上的任意实数![]() 分别满足:
分别满足: ![]() 和
和![]() ,则称直线
,则称直线![]() 为
为![]() 和
和![]() 的“隔离直线”.已知
的“隔离直线”.已知![]() ,
, ![]() 为自然对数的底数).
为自然对数的底数).
(1)求![]() 的极值;
的极值;
(2)函数![]() 和
和![]() 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com