
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 经过
经过![]() ,
, ![]() 两点,且圆心在直线
两点,且圆心在直线![]() 上.
上.
(1)求圆![]() 的标准方程;
的标准方程;
(2)过圆![]() 内一点
内一点![]() 作两条相互垂直的弦
作两条相互垂直的弦![]() ,当
,当![]() 时,求四边形
时,求四边形![]() 的面积.
的面积.
(3)设直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,
两点, ![]() ,且
,且![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)9;(3)
;(2)9;(3)![]() 或
或![]() .
.
【解析】试题分析:(1)由圆的方程可采用待定系数法或利用圆的性质:弦的垂直平分线过圆心等来求解;(2)将四边形面积用弦长表示,利用直线与圆相交时弦长一半,圆的半径,圆心到直线的距离构成的直角三角形求解;(3)设出直线方程![]() ,将弦长和面积用
,将弦长和面积用![]() 表示,解方程可得到直线
表示,解方程可得到直线![]() 的方程
的方程
试题解析:(1)因为![]() ,
, ![]() ,所以
,所以![]() ,AB的中点为
,AB的中点为![]() ,
,
故线段AB的垂直平分线的方程为![]() ,即
,即![]() ,
,
由![]() ,解得圆心坐标为
,解得圆心坐标为![]() .
.
所以半径r满足![]() .
.
故圆![]() 的标准方程为
的标准方程为![]() .
.
(2)∵![]() ∴
∴![]() 到直线
到直线![]() 的距离相等,设为
的距离相等,设为![]()
则![]()
∴![]()
∴四边形![]() 的面积
的面积![]()
(3)设坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,因为
,因为![]() .
.
①当直线![]() 与x轴垂直时,由坐标原点
与x轴垂直时,由坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() 知,直线
知,直线![]() 的方程为
的方程为![]()
或![]() ,经验证,此时
,经验证,此时![]() ,不适合题意;
,不适合题意;
②当直线![]() 与x轴不垂直时,设直线
与x轴不垂直时,设直线![]() 的方程为
的方程为![]() ,
,
由坐标原点到直线![]() 的距离为
的距离为![]() ,得
,得![]() (*),
(*),
又圆心到直线![]() 的距离为
的距离为![]() ,所以
,所以 ,
,
即![]() (**),
(**),
由(*),(**)解得 .
.
综上所述,直线![]() 的方程为
的方程为![]() 或
或![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】下图是甲、乙两人在一次射击比赛中中靶的情况(击中靶中心的圆面为10环,靶中各数字表示该数字所在圆环被击中所得的环数),每人射击了6次.

甲射击的靶 乙射击的靶
(1)请用列表法将甲、乙两人的射击成绩统计出来;
(2)请你用学过的统计知识,对甲、乙两人这次的射击情况进行比较.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=xex , 则( )
A.x=1为f(x)的极大值点
B.x=1为f(x)的极小值点
C.x=﹣1为f(x)的极大值点
D.x=﹣1为f(x)的极小值点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某公共汽车线路收支差额(票价总收人减去运营成本)与乘客量的函数图象.目前这条线路亏损,为了扭亏,有关部门举行提高票价的听证会.乘客代表认为:公交公司应节约能源,改善管理,降低运营成本,以此举实现扭亏.公交公司认为:运营成本难以下降,公司己尽力,提高票价才能扭亏.根据这两种意见,可以把图分别改画成图②和图③,
(1)说明图①中点![]() 和点
和点![]() 以及射线
以及射线![]() 的实际意义;
的实际意义;
(2)你认为图②和图③两个图象中,反映乘客意见的是_________,反映公交公司意见的是_________.
(3)如果公交公司采用适当提高票价又减少成本的办法实现扭亏为赢,请你在图④中画出符合这种办法的大致函数关系图象.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+bx2+cx+d的图象如图,则函数 ![]() 的单调递减区间是( )
的单调递减区间是( ) 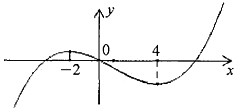
A.(﹣∞,﹣2)
B.(﹣∞,1)
C.(﹣2,4)
D.(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S—ABCD的底面为正方形,SD⊥底面ABCD,则下列结论
①AC⊥SB
②AB∥平面SCD
③SA与平面ABD所成的角等于SC与平面ABD所成的角
④AB与SC所成的角等于DC与SA所成的角.
⑤二面角![]() 的大小为
的大小为![]()
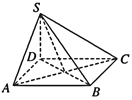
其中,正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学对高三学生进行体能测试,已知高三某文科班有学生30人,立定跳远的测试成绩用茎叶图表示如图(单位: ![]() );男生成绩在
);男生成绩在![]() 以上(包括
以上(包括![]() )定义为“合格”,成绩在
)定义为“合格”,成绩在![]() 以下(不包括
以下(不包括![]() )定义为“不合格”;女生成绩在
)定义为“不合格”;女生成绩在![]() 以上(包括
以上(包括![]() )定义为“合格”,成绩在
)定义为“合格”,成绩在![]() 以下(不包括
以下(不包括![]() )定义为“不合格.
)定义为“不合格.
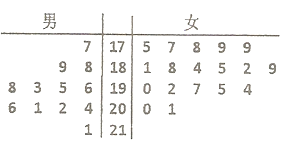
(1)求女生立定跳远测试成绩的中位数;
(2)若在男生中按成绩是否合格进行分层抽样,抽取6人,求抽取成绩为“合格”的学生人数;
(3)若从(2)中抽取的6名男生中任意选取4人,求这4人中至少有3人“合格”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+ ![]() ,其中函数f(x)的图象在点(1,f(1))处的切线方程为y=x﹣1.
,其中函数f(x)的图象在点(1,f(1))处的切线方程为y=x﹣1.
(1)若a= ![]() ,求函数f(x)的解析式;
,求函数f(x)的解析式;
(2)若f(x)≥g(x)在[1,+∞)上恒成立,求实数a的取值范围;
(3)证明:1+ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】x,y 满足约束条件  ,若 z=y﹣ax 取得最大值的最优解不唯一,则实数 a 的值为( )
,若 z=y﹣ax 取得最大值的最优解不唯一,则实数 a 的值为( )
A.![]() 或﹣1
或﹣1
B.2 或 ![]()
C.2 或1
D.2 或﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com