考点:棱柱、棱锥、棱台的体积,点、线、面间的距离计算
专题:空间位置关系与距离
分析:(1)以A为原点,AC为y轴,AA
1这z轴,建立空间直角坐标系,利用向量法能求出直线AC及A
1B
1的距离.
(2)求出平面A
1BC的法向量,利用向量法能求出点C
1到平面A
1BC的距离.
(3)求出
S△A1BC=
×2×=
,由此能求出三棱锥C
1-A
1BC的体积.
解答:
解:(1)以A为原点,
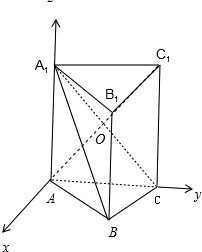
AC为y轴,AA
1这z轴,建立空间直角坐标系,
A(0,0,0),C(0,2,0),B(
,1,0),
A
1(0,0,2),B
1(
,1,2),C
1(0,2,2),
=(0,2,0),
=(
,1,0),
设异面直线AC及A
1B
1的公共法向量
=(x,y,z),
则
,∴
=(0,0,1),
=(0,0,2),
∴面直线AC及A
1B
1的距离d
1=
=
=2.
(2)
=(
,1,-2),
=(0,2,-2),
设平面A
1BC的法向量
=(a,b,c),
则
,取b=1,得
=(
,1,1),
=(0,2,0),
点C
1到平面A
1BC的距离d
2=
=
=
.
(3)∵
A1B=A1C==,BC=2,
∴
S△A1BC=
×2×=
,
∴三棱锥C
1-A
1BC的体积V=
S△A1BC•d2=
××=
.
点评:本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

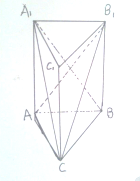 如图,正三棱柱ABC-A1B1C1的边长及棱的长度均为2,求:
如图,正三棱柱ABC-A1B1C1的边长及棱的长度均为2,求: AC为y轴,AA1这z轴,建立空间直角坐标系,
AC为y轴,AA1这z轴,建立空间直角坐标系,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案