
分析 可令x=y=0,求得f(0)=0,再由y=-x,可得f(x)为奇函数,由单调性的定义,可得f(x)为增函数,不等式f($\sqrt{x}$-log2x)>0,即为f($\sqrt{x}$-log2x)>f(0),即$\sqrt{x}$>log2x,画出函数的图象即可得到解集.
解答 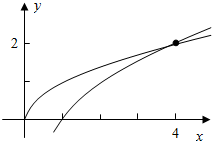 解:由f(x+y)=f(x)+f(y),
解:由f(x+y)=f(x)+f(y),
令x=y=0,可得f(0)=0,
令y=-x,可得f(0)=f(x)+f(-x)=0,
即f(x)为奇函数,
令m<n,即n-m>0,
由当x>0时,f(x)>0,可得f(n-m)>0,
即为f(n)+f(-m)>0,即f(n)-f(m)>0,
则f(x)为R上的增函数;
不等式f($\sqrt{x}$-log2x)>0,即为f($\sqrt{x}$-log2x)>f(0),
即有$\sqrt{x}$-log2x>0,即$\sqrt{x}$>log2x,
作出函数y=log2x,y=$\sqrt{x}$的图象,可得交点为(4,2),
可得不等式的解集为(0,4).
故答案为:(0,4).
点评 本题考查抽象函数的运用,考查函数的奇偶性和单调性的判断和应用:解不等式,注意运用图象,属于中档题.


科目:高中数学 来源: 题型:解答题
 船上两根高5m的桅杆相距10m,一条30m长的绳子两端系在桅杆的顶上,并按如图所示的方式绷紧,假设绳子位于两根桅杆所在的平面内,求绳子与甲板接触点P到桅杆AB的距离.
船上两根高5m的桅杆相距10m,一条30m长的绳子两端系在桅杆的顶上,并按如图所示的方式绷紧,假设绳子位于两根桅杆所在的平面内,求绳子与甲板接触点P到桅杆AB的距离.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com