
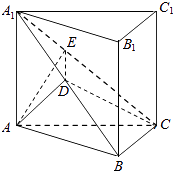
【题目】如图,在直三棱柱ABC﹣A1B1C1中,平面A1BC⊥侧面A1ABB1 , 且AA1=AB=2. 
(1)求证:AB⊥BC;
(2)若直线AC与平面A1BC所成的角为 ![]() ,求锐二面角A﹣A1C﹣B的大小.
,求锐二面角A﹣A1C﹣B的大小.
【答案】
(1)证明:如右图,取A1B的中点D,连接AD,
因AA1=AB,则AD⊥A1B
由平面A1BC⊥侧面A1ABB1,
且平面A1BC∩侧面A1ABB1=A1B,
得AD⊥平面A1BC,又BC平面A1BC,
所以AD⊥BC.
因为三棱柱ABC﹣﹣﹣A1B1C1是直三棱柱,
则AA1⊥底面ABC,
所以AA1⊥BC.
又AA1∩AD=A,从而BC⊥侧面A1ABB1,
又AB侧面A1ABB1,故AB⊥BC
(2)解:连接CD,由(1)可知AD⊥平面A1BC,
则CD是AC在平面A1BC内的射影
∴∠ACD即为直线AC与平面A1BC所成的角,则 ![]()
在等腰直角△A1AB中,AA1=AB=2,且点D是A1B中点
∴ ![]() ,且
,且 ![]() ,
, ![]()
∴ ![]()
过点A作AE⊥A1C于点E,连DE
由(1)知AD⊥平面A1BC,则AD⊥A1C,且AE∩AD=A
∴∠AED即为二面角A﹣A1C﹣B的一个平面角,
且直角△A1AC中: ![]()
又 ![]() ,
, ![]()
∴ ![]() ,
,
且二面角A﹣A1C﹣B为锐二面角
∴ ![]() ,即二面角A﹣A1C﹣B的大小为
,即二面角A﹣A1C﹣B的大小为 ![]() .
.
【解析】(1)取A1B的中点D,连接AD,由已知条件推导出AD⊥平面A1BC,从而AD⊥BC,由线面垂直得AA1⊥BC.由此能证明AB⊥BC.(2)连接CD,由已知条件得∠ACD即为直线AC与平面A1BC所成的角,∠AED即为二面角A﹣A1C﹣B的一个平面角,由此能求出二面角A﹣A1C﹣B的大小.
【考点精析】解答此题的关键在于理解空间中直线与直线之间的位置关系的相关知识,掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:
【题目】△ABC中A(3,﹣1),AB边上的中线CM所在直线方程为6x+10y﹣59=0,∠B的平分线方程BT为x﹣4y+10=0.
(1)求顶点B的坐标;
(2)求直线BC的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知菱形ABCD的顶点A,C在椭圆x2+3y2=4上,对角线BD所在直线的斜率为1.
(1)当直线BD过点(0,1)时,求直线AC的方程;
(2)当∠ABC=60°时,求菱形ABCD面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知Sn为等比数列{an}的前n项和且S4=S3+3a3 , a2=9.
(1)求数列{an}的通项公式
(2)设bn=(2n﹣1)an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上面图给出的是计算1+2+4+…+22017的值的一个程序框图,则其中判断框内应填入的是( ) 
A.i=2017?
B.i≥2017?
C.i≥2018?
D.i≤2018?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆M:x2+y2﹣2y=24,直线l:x+y=11,l上一点A的横坐标为a,过点A作圆M的两条切线l1 , l2 , 切点为B,C. 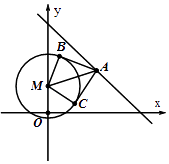
(1)当a=0时,求直线l1 , l2的方程;
(2)是否存在点A,使得 ![]() =﹣2?若存在,求出点A的坐标,若不存在,请说明理由.
=﹣2?若存在,求出点A的坐标,若不存在,请说明理由.
(3)求证当点A在直线l运动时,直线BC过定点P0 .
(附加题)问:第(3)问的逆命题是否成立?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=  .
.
(1)判断函数f(x)在区间(0,1)和[1,+∞)上的单调性(不必证明);
(2)当0<a<b,且f(a)=f(b)时,求 ![]() 的值;
的值;
(3)若存在实数a,b(1<a<b)使得x∈[a,b]时,f(x)的取值范围是[ma,mb](m≠0),求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC= ![]() ,O,M分别为AB,VA的中点.
,O,M分别为AB,VA的中点.
(1)求证:VB∥平面MOC;
(2)求证:平面MOC⊥平面VAB
(3)求三棱锥V﹣ABC的体积. 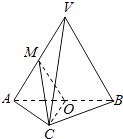
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,过焦点垂直与x轴的直线被椭圆E截得的线段长为
,过焦点垂直与x轴的直线被椭圆E截得的线段长为 ![]() .
.
(1)求椭圆E的方程;
(2)斜率为k的直线l经过原点,与椭圆E相交于不同的两点M,N,判断并说明在椭圆E上是否存在点P,使得△PMN的面积为 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com