
【题目】已知函数f(x)=|x﹣a|+|2x﹣a|(a∈R).
(1)若f(1)<11,求a的取值范围;
(2)若a∈R,f(x)≥x2﹣x﹣3恒成立,求x的取值范围.
【答案】
(1)解:f(1)=|1﹣a|+|2﹣a|= 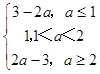 ,
,
当a≤1时,3﹣2a<11,解得a>﹣4,∴﹣4<a≤1;
当1<a<2时,1<11恒成立;
当a≥2时,2a﹣3<11,解得a<4,2≤a<4.
综上,a的取值范围是(﹣4,4)
(2)解:f(x)=|x﹣a|+|2x﹣a|≥|x﹣a﹣(2x﹣a)|=|x|,
∴|x|≥x2﹣x﹣3,
∴  或
或 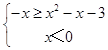 ,
,
解得0≤x≤ ![]() 或﹣
或﹣ ![]() x<0.
x<0.
∴﹣ ![]() ≤x≤
≤x≤ ![]()
【解析】(1)讨论a的范围,得出f(1)关于a的解析式,从而解出a的值;(2)把a看作自变量,利用绝对值三角不等式得出|x﹣a|+|2x﹣a|的最小值,从而得出关于x的不等式解出.
【考点精析】掌握绝对值不等式的解法是解答本题的根本,需要知道含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


科目:高中数学 来源: 题型:
【题目】设函数 ![]() ,若曲线
,若曲线 ![]() 上存在(x0 , y0),使得f(f(y0))=y0成立,则实数m的取值范围为( )
上存在(x0 , y0),使得f(f(y0))=y0成立,则实数m的取值范围为( )
A.[0,e2﹣e+1]
B.[0,e2+e﹣1]
C.[0,e2+e+1]
D.[0,e2﹣e﹣1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+2|+|x﹣1|.
(1)求不等式f(x)>5的解集;
(2)若对于任意的实数x恒有f(x)≥|a﹣1|成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=g(x)﹣(a﹣1)lnx,g(x)=ax+ ![]() +1﹣3a+(a﹣1)lnx.
+1﹣3a+(a﹣1)lnx.
(1)当a=1时,求函数y=f(x)在点(2,f(2))处的切线方程;
(2)若不等式g(x)≥0在x∈[1,+∞)时恒成立,求正实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司的研发团队,可以进行A、B、C三种新产品的研发,研发成功的概率分别为P(A)= ![]() ,P(B)=
,P(B)= ![]() ,P(C)=
,P(C)= ![]() ,三个产品的研发相互独立.
,三个产品的研发相互独立.
(1)求该公司恰有两个产品研发成功的概率;
(2)已知A、B、C三种产品研发成功后带来的产品收益(单位:万元)分别为1000、2000、1100,为了收益最大化,公司从中选择两个产品研发,请你从数学期望的角度来考虑应该研发哪两个产品?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax(a为常数)的图象与y轴交于点A,曲线y=f(x)在点A处的切线斜率为﹣1.
(1)求a的值及函数f(x)的极值;
(2)证明:当x>0时,x2<ex;
(3)证明:对任意给定的正数c,总存在x0 , 使得当x∈(x0 , +∞)时,恒有x<cex .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将正方形ABCD沿对角线BD折成直二面角后的图形如图所示,若E为线段BC的中点,则直线AE与平面ABD所成角的余弦为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com