
| A. | $\frac{1}{2}$或$\frac{3}{2}$ | B. | 1 | C. | 1或$\frac{1}{2}$ | D. | $\frac{3}{2}$ |
分析 根据题意画出图形,结合图形求出AB、OD的长,再根据数量积与投影的定义,列出方程求出结果.
解答 解:如图所示,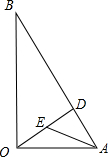
∵$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,∴$\overrightarrow{OA}$⊥$\overrightarrow{OB}$,即OA⊥OB,
∴AB=$\sqrt{{OA}^{2}{+OB}^{2}}$=5;
又OD为AB边上的高,
∴OD⊥AB,
∴OD=$\frac{OA×OB}{AB}$=$\frac{\sqrt{5}×2\sqrt{5}}{5}$=2,
∴$\overrightarrow{OE}$•$\overrightarrow{EA}$=|$\overrightarrow{OE}$|•|$\overrightarrow{EA}$|cos∠AED=|$\overrightarrow{OE}$|•|$\overrightarrow{ED}$|=$\frac{3}{4}$;
设|$\overrightarrow{ED}$|为x,则x(2-x)=$\frac{3}{4}$,
解得x=$\frac{1}{2}$或x=$\frac{3}{2}$,
∴向量$\overrightarrow{EA}$在向量$\overrightarrow{OD}$上的投影为|$\overrightarrow{ED}$|=$\frac{1}{2}$或$\frac{3}{2}$.
故选:A.
点评 本题主要考查平面向量的数量积与向量投影的定义和应用问题,是综合性题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+y-5=0 | B. | 2x+y+5=0 | C. | 2x-y-5=0 | D. | 2x-y+5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
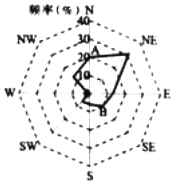 如图所示为某城市去年风向频率图,图中A点表示该城市去年有的天数吹北风,点表示该城B市去年有10%的天数吹东南风,下面叙述不正确的是( )
如图所示为某城市去年风向频率图,图中A点表示该城市去年有的天数吹北风,点表示该城B市去年有10%的天数吹东南风,下面叙述不正确的是( )| A. | 去年吹西北风和吹东风的频率接近 | B. | 去年几乎不吹西风 | ||
| C. | 去年吹东风的天数超过100天 | D. | 去年吹西南风的频率为15%左右 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
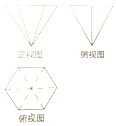 一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的体积是( )
一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的体积是( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com