
【题目】已知函数f(x)=ax2+2x﹣2﹣a(a≤0),
(1)若a=﹣1,求函数的零点;
(2)若函数在区间(0,1]上恰有一个零点,求a的取值范围.
【答案】(1)当a=﹣1时,函数f(x)的零点是1;(2)﹣1≤a≤0或a≤﹣2.
【解析】试题分析:(1)令f(x)=﹣x2+2x﹣1=0,求解即可;
(2)讨论当a=0时和当a<0时二次函数在区间(0,1]的零点分别求参数范围即可.
试题解析:
(1)当a=﹣1时,f(x)=﹣x2+2x﹣1,
令f(x)=﹣x2+2x﹣1=0,
解得x=1,
∴当a=﹣1时,函数f(x)的零点是1.
(2)①当a=0时,2x﹣2=0得x=1,符合题意.
②当a<0时,f(x)=ax2+2x﹣2﹣a=a(x﹣1)(x+![]() ),
),
则x1=1,x2=﹣![]() ,
,
由于函数在区间(0,1]上恰有一个零点,则﹣![]() ≥1或﹣
≥1或﹣![]() ≤0,
≤0,
解得﹣1≤a<0或a≤﹣2,
综上可得,a的取值范围为﹣1≤a≤0或a≤﹣2.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2ax+5(a>1).
(1)若f(x)的定义域和值域均是[1,a],求实数a的值;
(2)若f(x)在区间(﹣∞,2]上是减函数,且对任意的x∈[1,a+1],总有f(x)≤0,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,多面体PABCD的直观图及三视图如图所示,E、F分别为PC、BD的中点.

(I)求证:EF∥平面PAD;
(II)求证:平面PDC⊥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左、右焦点分别为F1、F2 , |F1F2|=4,P是双曲线右支上一点,直线PF2交y轴于点A,△APF1的内切圆切边PF1于点Q,若|PQ|=1,则双曲线的离心率为 .
=1(a>0,b>0)的左、右焦点分别为F1、F2 , |F1F2|=4,P是双曲线右支上一点,直线PF2交y轴于点A,△APF1的内切圆切边PF1于点Q,若|PQ|=1,则双曲线的离心率为 . 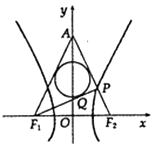
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ,g(x)=lnx+
,g(x)=lnx+ ![]() (a>0).
(a>0).
(1)求函数f(x)的极值;
(2)若x1、x2∈(0,+∞),使得g(x1)≤f(x2)成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ,若f(a)=f(b)=f(c)=f(d),其中a,b,c,d互不相等,则对于命题p:abcd∈(0,1)和命题q:a+b+c+d∈[e+e﹣1﹣2,e2+e﹣2﹣2)真假的判断,正确的是( )
,若f(a)=f(b)=f(c)=f(d),其中a,b,c,d互不相等,则对于命题p:abcd∈(0,1)和命题q:a+b+c+d∈[e+e﹣1﹣2,e2+e﹣2﹣2)真假的判断,正确的是( )
A.p假q真
B.p假q假
C.p真q真
D.p真q假
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的首项a1=1,且(n+1)a ![]() +anan+1﹣na
+anan+1﹣na ![]() =0对n∈N*都成立.
=0对n∈N*都成立.
(1)求{an}的通项公式;
(2)记bn=a2n﹣1a2n+1 , 数列{bn}的前n项和为Tn , 证明:Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y=f(x)图象上不同两点A(x1 , y1),B(x2 , y2)处的切线的斜率分别是kA , kB , 规定φ(A,B)= ![]() (|AB|为线段AB的长度)叫做曲线y=f(x)在点A与点B之间的“弯曲度”,给出以下命题: ①函数y=x3图象上两点A与B的横坐标分别为1和﹣1,则φ(A,B)=0;
(|AB|为线段AB的长度)叫做曲线y=f(x)在点A与点B之间的“弯曲度”,给出以下命题: ①函数y=x3图象上两点A与B的横坐标分别为1和﹣1,则φ(A,B)=0;
②存在这样的函数,图象上任意两点之间的“弯曲度”为常数;
③设点A,B是抛物线y=x2+1上不同的两点,则φ(A,B)≤2;
④设曲线y=ex(e是自然对数的底数)上不同两点A(x1 , y1),B(x2 , y2),则φ(A,B)<1.
其中真命题的序号为 . (将所有真命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为招聘新员工设计了一个面试方案:应聘者从6道备选题中一次性随机抽取3道题,按照题目要求独立完成.规定:至少正确完成其中2道题的便可通过.已知6道备选题中应聘者甲有4道题能正确完成,2道题不能完成;应聘者乙每题正确完成的概率都是 ![]() ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(Ⅰ)分别求甲、乙两人正确完成面试题数的分布列,并计算其数学期望;
(Ⅱ)请分析比较甲、乙两人谁的面试通过的可能性大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com