
【题目】某公司组织开展“学习强国”的学习活动,活动第一周甲、乙两个部门员工的学习情况统计如下:
学习活跃的员工人数 | 学习不活跃的员工人数 | |
甲 | 18 | 12 |
乙 | 32 | 8 |
(1)从甲、乙两个部门所有员工中随机抽取1人,求该员工学习活跃的概率;
(2)根据表中数据判断能否有![]() 的把握认为员工学习是否活跃与部门有关;
的把握认为员工学习是否活跃与部门有关;
(3)活动第二周,公司为检查学习情况,从乙部门随机抽取2人,发现这两人学习都不活跃,能否认为乙部门第二周学习的活跃率比第一周降低了?
参考公式: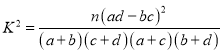 ,其中
,其中![]() .
.
参考数据:![]() ,
,![]() ,
,![]() .
.
【答案】(1)![]() ;(2)没有;(3)见解析
;(2)没有;(3)见解析
【解析】
(1)根据两个部门员工的总数和学习活跃的人数,利用古典概型求解;
(2)根据公式计算出![]() 即可判定;
即可判定;
(3)根据随机事件的发生具有偶然性以及概率大小关系,言之成理即可.
(1)设事件![]() 为“从甲、乙两个部门所有员工中随机抽取1人,该员工学习活跃”.
为“从甲、乙两个部门所有员工中随机抽取1人,该员工学习活跃”.
则![]() .
.
(2)![]() .
.
因为![]() ,所以没有
,所以没有![]() 的把握认为员工学习是否活跃与部门有关.
的把握认为员工学习是否活跃与部门有关.
(3)设事件![]() 为“第二周从乙部门随机抽取2人,这两人学习都不活跃”.
为“第二周从乙部门随机抽取2人,这两人学习都不活跃”.
若第二周保持第一周的活跃情况,则![]() .
.
答案示例一:可以认为活跃率降低了,因为![]() 很小,事件
很小,事件![]() 一般不容易发生,现在发生了,则说明学习不活跃的人数增加了,即活跃率降低了.
一般不容易发生,现在发生了,则说明学习不活跃的人数增加了,即活跃率降低了.
答案示例二:不能认为活跃率降低了.因为事件![]() 是随机事件,虽然
是随机事件,虽然![]() 较小,但还是有可能发生,所以不能认为活跃率降低.
较小,但还是有可能发生,所以不能认为活跃率降低.


科目:高中数学 来源: 题型:
【题目】如图,已知四边形ABCD是正方形,AE⊥平面ABCD,PD∥AE,PD=AD=2EA=2,G,F,H分别为BE,BP,PC的中点.
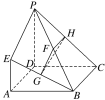
(1)求证:平面ABE⊥平面GHF;
(2)求直线GH与平面PBC所成的角θ的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“二万五千里长征”是1934年10月到1936年10月中国工农红军进行的一次战略转移,是人类历史上的伟大奇迹,向世界展示了中国工农红军的坚强意志,在期间发生了许多可歌可泣的英雄故事.在中国共产党建党![]() 周年之际,某中学组织了“长征英雄事迹我来讲”活动,已知该中学共有高中生
周年之际,某中学组织了“长征英雄事迹我来讲”活动,已知该中学共有高中生![]() 名,用分层抽样的方法从该校高中学生中抽取一个容量为
名,用分层抽样的方法从该校高中学生中抽取一个容量为![]() 的样本参加活动,其中高三年级抽了
的样本参加活动,其中高三年级抽了![]() 人,高二年级抽了
人,高二年级抽了![]() 人,则该校高一年级学生人数为( )
人,则该校高一年级学生人数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在五面体ABCDPN中,棱PA⊥面ABCD,AB=AP=2PN,底面ABCD是菱形,∠BAD=![]() .
.

(1)求证:PN∥AB;
(2)求NC与平面BDN所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若曲线![]() 上一点
上一点![]() 的极坐标为
的极坐标为![]() ,且
,且![]() 过点
过点![]() ,求
,求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,
,![]() 与
与![]() 的交点为
的交点为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个排球队在采用![]() 局
局![]() 胜制排球决赛中相遇,已知每局比赛中甲获胜的概率是
胜制排球决赛中相遇,已知每局比赛中甲获胜的概率是![]() .
.
(1)求比赛进行了![]() 局就结束的概率;
局就结束的概率;
(2)若第![]() 局甲胜,两队又继续进行了
局甲胜,两队又继续进行了![]() 局结束比赛,求
局结束比赛,求![]() 的分布列和数学期望
的分布列和数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() )的图象为曲线
)的图象为曲线![]() .
.
(Ⅰ)求曲线![]() 上任意一点处的切线的斜率的取值范围;
上任意一点处的切线的斜率的取值范围;
(Ⅱ)若曲线![]() 上存在两点处的切线互相垂直,求其中一条切线与曲线
上存在两点处的切线互相垂直,求其中一条切线与曲线![]() 的切点的横坐标的取值范围;
的切点的横坐标的取值范围;
(Ⅲ)试问:是否存在一条直线与曲线C同时切于两个不同点?如果存在,求出符合条件的所有直线方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com