
【题目】如图所示,已知![]() 为圆
为圆![]() 的直径,点
的直径,点![]() 为线段
为线段![]() 上一点,且
上一点,且![]() ,点
,点![]() 为圆
为圆![]() 上一点,且
上一点,且![]() .点
.点![]() 在圆
在圆![]() 所在平面上的正投影为点
所在平面上的正投影为点![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析;(2)![]()
【解析】
试题(1)先利用平面几何知识与线面垂直的性质证线线垂直,由线线垂直得到线面垂直,再由线面垂直得到线线垂直;(2)建立空间坐标系,利用向量法求解即可.
试题解析:(1)如图,连接![]() ,
,
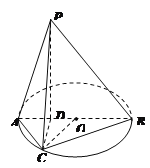
由![]() 知,点
知,点![]() 为
为![]() 的中点,
的中点,
又∵![]() 为圆
为圆![]() 的直径,
的直径,
∴![]() ,
,
由![]() 知,
知,![]() ,
,
∴![]() 为等边三角形,从而
为等边三角形,从而![]() .
.
∵点![]() 在圆
在圆![]() 所在平面上的正投影为点
所在平面上的正投影为点![]() ,
,
∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
∴![]() ,
,
由![]() 得,
得,![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
∴![]() .
.
(2)以![]() 为原点,
为原点,![]() 、
、![]() 和
和![]() 的方向分别为
的方向分别为![]() 轴、
轴、![]() 轴和
轴和![]() 轴的正向,建立如图所示的空间直角坐标系,
轴的正向,建立如图所示的空间直角坐标系,
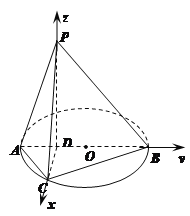
设![]() ,由
,由![]() ,
,![]() 得,
得,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
由![]() 平面
平面![]() ,知平面
,知平面![]() 的一个法向量为
的一个法向量为![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则
 ,即
,即 ,令
,令![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,
设二面角![]() 的平面角的大小为
的平面角的大小为![]() ,
,
则 ,
,
∴二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】在一次购物抽奖活动中,假设某10张券中有一等奖券2张,每张可获价值50元的奖品;有二等奖券2张,每张可获价值10元的奖品;其余6张没有奖.某顾客从此10张奖券中任抽2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值X元的概率分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出下列四个结论:
,给出下列四个结论:
① 函数![]() 的最小正周期是
的最小正周期是![]() ;
;
② 函数![]() 在区间
在区间![]() 上是减函数;
上是减函数;
③ 函数![]() 的图像关于点
的图像关于点![]() 对称;
对称;
④ 函数![]() 的图像可由函数
的图像可由函数![]() 的图像向右平移
的图像向右平移![]() 个单位,再向下平移1个单位得到.其中正确结论的个数是( )
个单位,再向下平移1个单位得到.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为庆祝党的98岁生日,某高校组织了“歌颂祖国,紧跟党走”为主题的党史知识竞赛。从参加竞赛的学生中,随机抽取40名学生,将其成绩分为六段![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,到如图所示的频率分布直方图.
,到如图所示的频率分布直方图.

(1)求图中![]() 的值及样本的中位数与众数;
的值及样本的中位数与众数;
(2)若从竞赛成绩在![]() 与
与![]() 两个分数段的学生中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于
两个分数段的学生中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于![]() 分为事件
分为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
(3)为了激励同学们的学习热情,现评出一二三等奖,得分在![]() 内的为一等奖,得分在
内的为一等奖,得分在![]() 内的为二等奖, 得分在
内的为二等奖, 得分在![]() 内的为三等奖.若将频率视为概率,现从考生中随机抽取三名,设
内的为三等奖.若将频率视为概率,现从考生中随机抽取三名,设![]() 为获得三等奖的人数,求
为获得三等奖的人数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有2002名运动员,号码依次为![]() .从中选出若干名运动员参加仪仗队,但要使剩下的运动员中没有一个人的号码数等于另外两人的号码数的乘积.那么,被选为仪仗队的运动员至少能有多少人?给出你的选取方案,并简述理由.
.从中选出若干名运动员参加仪仗队,但要使剩下的运动员中没有一个人的号码数等于另外两人的号码数的乘积.那么,被选为仪仗队的运动员至少能有多少人?给出你的选取方案,并简述理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com