练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．已知曲线y=f（x）在x=5处的切线方程是y=-x+5，则f（5）与f'（5）分别为（　　）
    A．3，3B．3，-1C．-1，3D．0，-1

    分析 利用导数的几何意义得到f'（5）等于直线的斜率-1，由切点横坐标为5，得到纵坐标即f（5）．

    解答 解：由题意得f（5）=-5+5=0，f′（5）=-1．
    故选：D．

    点评 本题考查了导数的几何意义，考查学生的计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    17．将圆x2+y2=1上每一点的纵坐标保持不变，横坐标变为原来的2倍，得到曲线C．
    （1）写出曲线C的参数方程；
    （2）过点$N（\sqrt{3}，0）$的直线l与C的交点为A，B，与y轴交于点M，且$\overrightarrow{AM}={λ_1}\overrightarrow{AN}$，$\overrightarrow{BM}={λ_2}\overrightarrow{BN}$，求λ1+λ2的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．（1）已知tanα=3，计算$\frac{3sinα+cosα}{sinα-2cosα}$；
    （2）若cos（α+β）=$\frac{1}{5}$，cos（α-β）=$\frac{3}{5}$，求tanα•tanβ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．下列命题中：
    ①命题p：“?x0∈R，${x_0}^2-{x_0}-1＞0$”的否定?p“?x∈R，x2-x-1≤0”；
    ②汽车的重量和汽车每消耗1升汽油所行驶的平均路程成正相关关系；
    ③命题“若a＞b，则2a＞2b-1”的否命题为“若a≤b，则2a≤2b-1”；
    ④概率是随机的，在试验前不能确定．
    正确的有①③．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．命题“?x＞0，ex-x-1≥0”的否定是?x＞0，ex-x-1＜0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．（1）已知函数f（x）=x3-mx2-nx的图象与x轴相切，切点为（1，0），且g（x）=f（x）+1，求g（x）的极值．
    （2）已知f（x）=ax2+bx+c（a≠0），且f（-1）=2，f'（0）=0，$\int_{\;-1}^{\;0}{f（x）dx=-4}$，求a、b、c的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知函数f（x）定义域为[0，+∞），当x∈[0，1]时，f（x）=sinπx，当x∈[n，n+1]时，f（x）=$\frac{f（x-n）}{{2}^{n}}$，其中n∈N，若函数f（x）的图象与直线y=b有且仅有2016个交点，则b的取值范围是（　　）
    A．（0，1）B．（$\frac{1}{{2}^{1007}}$，$\frac{1}{{2}^{1006}}$）C．（$\frac{1}{{2}^{2017}}$，$\frac{1}{{2}^{2016}}$）D．（$\frac{1}{{2}^{1008}}$，$\frac{1}{{2}^{1007}}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．在平面直角坐标系中，点P为曲线C上任意一点，且P到定点F（1，0）的距离比到y轴的距离多1．
    （1）求曲线C的方程；
    （2）点M为曲线C上一点，过点M分别作倾斜角互补的直线MA，MB与曲线C分别交于A，B两点，过点F且与AB垂直的直线l与曲线C交于D，E两点，若|DE|=8，求点M的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

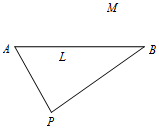    10．我边防局接到情报，在海礁AB所在直线l的一侧点M处有走私团伙在进行交易活动，边防局迅速派出快艇前去搜捕．如图，已知快艇出发位置在l的另一侧码头P处，PA=8公里，PB=10公里，∠APB=60°．
    （1）是否存在点M，使快艇沿航线P→A→M或P→B→M的路程相等．如存在，则建立适当的直角坐标系，求出点M的轨迹方程，且画出轨迹的大致图形；如不存在，请说明理由．
    （2）问走私船在怎样的区域上时，路线P→A→M比路线P→B→M的路程短，请说明理由．

    查看答案和解析>>

    同步练习册答案