
 如图所示,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等腰梯形,等腰直角三角形和长方形,则该几何体表面积为$4\sqrt{2}$+6+$\sqrt{3}$.
如图所示,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等腰梯形,等腰直角三角形和长方形,则该几何体表面积为$4\sqrt{2}$+6+$\sqrt{3}$. 分析 如图所示,分别经过点E,F,作EG⊥AB,EH⊥CD,EK⊥AB,EL⊥CD,垂足分别为:G,H,K,L.
则EH=EG=1,EF=2,AB=4.EG⊥EH,EF∥平面ABCD,四边形ABFE,CDEF为等腰梯形,ABCD为矩形,△ADE与△BCF是边长为$\sqrt{2}$的等边三角形.即可得出.
解答 解:如图所示,分别经过点E,F,作EG⊥AB,EH⊥CD,EK⊥AB,EL⊥CD,
垂足分别为:G,H,K,L.
则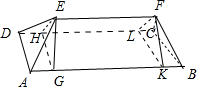 EH=EG=1,EF=2,AB=4.
EH=EG=1,EF=2,AB=4.
EG⊥EH,EF∥平面ABCD,四边形ABFE,CDEF为等腰梯形,ABCD为矩形,△ADE与△BCF是边长为$\sqrt{2}$的等边三角形.
∴该几何体表面积=$4\sqrt{2}$+2×$\frac{2+4}{2}×1$+$2×\frac{\sqrt{3}}{4}×(\sqrt{2})^{2}$
=$4\sqrt{2}$+6+$\sqrt{3}$.
故答案为:$4\sqrt{2}$+6+$\sqrt{3}$.
点评 本题考查了三视图的应用、三角形与梯形及其矩形面积计算公式,考查了推理能力与计算能力,属于中档题.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
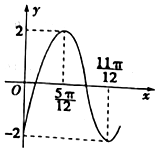 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
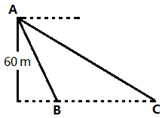 如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为60o,30°,此时气球的高是60m,则河流的宽度BC等于( )
如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为60o,30°,此时气球的高是60m,则河流的宽度BC等于( )| A. | $30\sqrt{3}$ | B. | $30({\sqrt{3}-1})$ | C. | $40\sqrt{3}$ | D. | $40({\sqrt{3}-1})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com