Question

【题目】已知F1 ， F2为椭圆 的左、右焦点，F2在以 为圆心，1为半径的圆C2上，且|QF1|+|QF2|=2a．

（1）求椭圆C1的方程；
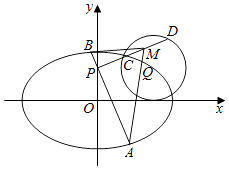
（2）过点P（0，1）的直线l1交椭圆C1于A，B两点，过P与l1垂直的直线l2交圆C2于C，D两点，M为线段CD中点，求△MAB面积的取值范围．

Answer 1

【答案】
（1）解：圆C2的方程为 ，

此圆与x轴相切，切点为

∴ ，即a2﹣b2=2，且 ，

又|QF1|+|QF2|=3+1=2a

∴a=2，b2=a2﹣c2=2

∴椭圆C1的方程为 ．

（2）解：当l1平行x轴的时候，l2与圆C2无公共点，从而△MAB不存在；

设l1：x=t（y﹣1），则l2：tx+y﹣1=0．

由 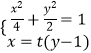，消去x得（t2+2）y2﹣2t2y+t2﹣4=0，

则 ．

又圆心 到l2的距离 ，得t2＜1．

又MP⊥AB，QM⊥CD

∴M到AB的距离即Q到AB的距离，设为d2，

即 ．

∴△MAB面积

令

则 ．

∴△MAB面积的取值范围为 ．

【解析】（1）圆C2的方程为 ，由此圆与x轴相切，求出a，b的值，由此能求出椭圆C1的方程．（2）设l1：x=t（y﹣1），则l2：tx+y﹣1=0，与椭圆联立，得（t2+2）y2﹣2t2y+t2﹣4=0，由此利用弦长公式、点到直线距离公式，结合已知条件能求出△MAB面积的取值范围．