
【题目】已知函数![]() .
.
(1)判断函数![]() 在区间
在区间![]() 上零点的个数,并说明理由.
上零点的个数,并说明理由.
(2)当![]() 时,
时,
①比较![]() 与
与![]() 的大小关系,并说明理由;
的大小关系,并说明理由;
②证明:![]() .
.
【答案】(1)有唯一一个零点,理由详见解析;(2)①![]() ,证明详见解析;②证明见解析.
,证明详见解析;②证明见解析.
【解析】
(1)先对函数求导,然后结合导数可判断函数的单调性,结合函数的性质可求函数的零点个数;
(2)①令![]() ,然后对其求导,结合导数可研究函数的单调性,进而由函数的取值范围可比较大小;
,然后对其求导,结合导数可研究函数的单调性,进而由函数的取值范围可比较大小;
②结合①的结论,利用分析法分析结论成立的条件,然后利用导数可求.
(1)因为![]() ,所以
,所以![]() .
.
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,且
,且![]() ,故
,故![]() 在
在![]() 上无零点;
上无零点;
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递减,
上单调递减,
又由![]() ,
,
故![]() 在区间
在区间![]() 上有唯一零点;
上有唯一零点;
综上,函数![]() 在区间
在区间![]() 上有唯一一个零点.
上有唯一一个零点.
(2)①![]() ,证明过程如下:
,证明过程如下:
设函数![]() ,则
,则![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]() ;
;
令![]() ,即
,即![]() ,解得
,解得![]() ,
,
所以函数![]() 在区间(0,1)上单调递减,在区间(1,π)上单调递增.
在区间(0,1)上单调递减,在区间(1,π)上单调递增.
则函数![]() 在
在![]() 处取得极小值,亦即最小值
处取得极小值,亦即最小值![]() ,
,
即![]() ,
,
综上可得,![]() 成立;
成立;
②要证:ln[f(x)]+1![]() ecosxf(x)﹣cosx成立,
ecosxf(x)﹣cosx成立,
即证明ln(sinx﹣xcosx)![]() (sinx﹣xcosx)ecosx﹣cosx﹣1成立,
(sinx﹣xcosx)ecosx﹣cosx﹣1成立,
因为f(x)在(0,π)上单调递增,![]() ,
,
即sinx﹣xcosx>0,所以(sinx﹣xcosx)ecosx>0,
由①知![]() ,即有
,即有![]() ,
,
有(sinx﹣xcosx)ecosx≥1+ln[(sinx﹣xcosx)ecosx]成立,
当![]() 时,
时,![]() 成立,
成立,
由![]() 成立,
成立,
此时能取等号,即有![]() 成立,
成立,
即![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】某综艺节目为比较甲、乙两名选手的各项能力(指标值满分为5分,分值高者为优),分别绘制了如图所示的六维能力雷达图,图中点A表示甲的创造力指标值为4,点B表示乙的空间能力指标值为3,则下列叙述错误的是( )
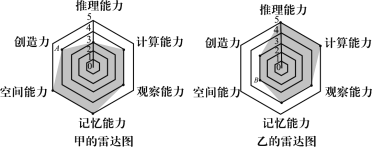
A.甲的六大能力中推理能力最差B.甲的创造力优于观察能力
C.乙的计算能力优于甲的计算能力D.乙的六大能力整体水平低于甲
查看答案和解析>>
科目:高中数学 来源: 题型:
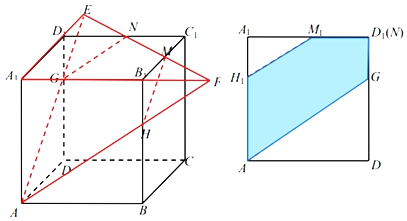
【题目】在棱长为1的正方体ABCD﹣A1B1C1D1中,点M,N分别是棱B1C1,C1D1的中点,过A,M,N三点作正方体的截面,将截面多边形向平面ADD1A1作投影,则投影图形的面积为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据国家统计局数据:2000年,2018年我国GDP(国内生产总值)分别为10万亿,90万亿.2000年与2018年国内生产总值中第一产业、第二产业、第三产生的比例如图,则对比2000年与2018年的数据,下列说法错误的是( )
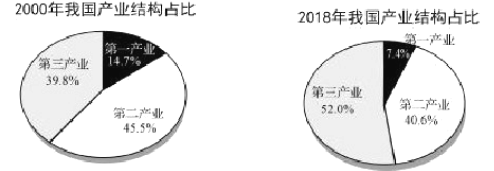
A.第一产业占比减少了约一半B.第二产业占比变化最小
C.第三产业生产总值增长了约11倍D.第一产业生产总值变化量最大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数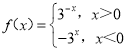 ,若
,若![]() ,b=f(log24.2),c=f(20.7),则a,b,c的大小关系为( )
,b=f(log24.2),c=f(20.7),则a,b,c的大小关系为( )
A.a<b<cB.b<a<cC.c<a<bD.c<b<a
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四个人到![]() ,
,![]() ,
,![]() 三个景点旅游,每个人只去一个景点,每个景点至少有一个人去,则甲不到
三个景点旅游,每个人只去一个景点,每个景点至少有一个人去,则甲不到![]() 景点的方案有( )
景点的方案有( )
A.18种B.12种C.36种D.24种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋中装有大小相同的5个小球,编号分别为0,1,2,3,4,现从中随机地摸一个球,记下编号后放回,连摸3次,若摸出的3个小球的最大编号与最小编号之差为2,则共有________种不同的摸球方法(用数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一排10个位置的空停车场,甲、乙、丙三辆不同的车去停放,要求每辆车左右两边都有空车位且甲车在乙、丙两车之间的停放方式共有_________种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在实数k,b,使得函数![]() 和
和![]() 对其定义域上的任意实数x同时满足:
对其定义域上的任意实数x同时满足:![]() 且
且![]() ,则称直线:
,则称直线:![]() 为函数
为函数![]() 和
和![]() 的“隔离直线”.已知
的“隔离直线”.已知![]() ,
,![]() (其中e为自然对数的底数).试问:
(其中e为自然对数的底数).试问:
(1)函数![]() 和
和![]() 的图象是否存在公共点,若存在,求出交点坐标,若不存在,说明理由;
的图象是否存在公共点,若存在,求出交点坐标,若不存在,说明理由;
(2)函数![]() 和
和![]() 是否存在“隔离直线”?若存在,求出此“隔离直线”的方程;若不存在,请说明理由.
是否存在“隔离直线”?若存在,求出此“隔离直线”的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com