
【题目】已知函数![]() .
.
(1)过点![]() (e是自然对数的底数)作函数
(e是自然对数的底数)作函数![]() 图象的切线l,求直线l的方程;
图象的切线l,求直线l的方程;
(2)求函数![]() 在区间
在区间![]() (
(![]() )上的最大值;
)上的最大值;
(3)若![]() ,且
,且![]() 对任意
对任意![]() 恒成立,求k的最大值.(参考数据:
恒成立,求k的最大值.(参考数据:![]() ,
,![]() )
)
【答案】(1)![]() (2)
(2)![]() (3)最大值是4.
(3)最大值是4.
【解析】
(1)设出切点坐标为![]() ,求得导函数后,将横坐标带入可得切线的斜率.点
,求得导函数后,将横坐标带入可得切线的斜率.点![]() 在切线方程上,可由点斜式表示出切线方程.带入切点后,可求得切点的横坐标.带入切线方程即可求解.
在切线方程上,可由点斜式表示出切线方程.带入切点后,可求得切点的横坐标.带入切线方程即可求解.
(2)求得导函数,并令![]() .即可求得极值点,并根据导函数符号判断出为极小值点.讨论
.即可求得极值点,并根据导函数符号判断出为极小值点.讨论![]() 及
及![]() 两种情况,即可根据单调性求得最大值.
两种情况,即可根据单调性求得最大值.
(3)因为![]() 时
时![]() ,分类参数
,分类参数![]() .构造函数
.构造函数![]() ,求得导函数
,求得导函数 ,并令
,并令![]() ,再求得
,再求得![]() .通过
.通过![]() 的符号,判断出
的符号,判断出![]() 的单调性.从而由零点存在定理可知
的单调性.从而由零点存在定理可知![]() 在
在![]() 上有且仅有一个零点.设这个零点为
上有且仅有一个零点.设这个零点为![]() ,结合
,结合![]() 函数可判断出当
函数可判断出当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .从而可知
.从而可知![]() 在
在![]() 处取得最小值.即可由整数
处取得最小值.即可由整数![]() 求得
求得![]() 的最大值.
的最大值.
(1)设切点为![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() ,
,
因为切线过点![]() ,所以切线方程为
,所以切线方程为![]() ,①
,①
代入切点![]() 得,
得,![]() ,
,
解得![]() ,代入①得直线l的方程为
,代入①得直线l的方程为![]() ,
,
即直线l的方程为![]() .
.
(2)函数![]() ,则
,则![]()
由![]() 得,
得,![]() ,
,
所以当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 是极小值,
是极小值,
因为![]() (
(![]() )恒成立,所以分如下两种情况讨论:
)恒成立,所以分如下两种情况讨论:
1°当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是增函数,
上是增函数,
则![]() ,
,
2°当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是增函数,
上是增函数,
则![]() ,
,
因为![]() ,
,
![]() 显然,
显然,
所以![]() ,
,
综上所述![]() 的最大值为
的最大值为![]() .
.
(3)由![]() 可知
可知![]() ,所以
,所以![]() 等价于
等价于![]() ,
,
令![]() ,则
,则 ,
,
令![]() ,则
,则![]() ,
,![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上是增函数,
上是增函数,
又因为![]() ,
,![]() ,
,
所以![]() 在
在![]() 上有且仅有一个零点,
上有且仅有一个零点,
记该零点为![]() ,
,![]()
所以![]() ,也即
,也即![]() ,
,
所以当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 处取得极小值,也是最小值,
处取得极小值,也是最小值,
即 ,
,
所以整数![]() (
(![]() ),
),
所以k的最大值是4.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】命题甲:“一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,则这两个二面角相等或互补.”命题乙:“底面为正三角形,侧面为等腰三角形的三棱锥是正三棱锥.”命题丙:“过圆锥的两条母线的截面,以轴截面的面积最大.”其中真命题的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
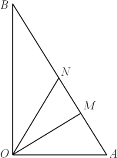
【题目】如图,某镇有一块空地![]() ,其中
,其中![]() ,
,![]() ,
,![]() .当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖
.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖![]() ,其中M,N都在边
,其中M,N都在边![]() 上,且
上,且![]() ,挖出的泥土堆放在
,挖出的泥土堆放在![]() 地带上形成假山,剩下的
地带上形成假山,剩下的![]() 地带开设儿童游乐场.为安全起见,需在
地带开设儿童游乐场.为安全起见,需在![]() 的周围安装防护网.
的周围安装防护网.
(1)当![]() 时,求防护网的总长度;
时,求防护网的总长度;
(2)为节省资金投入,人工湖![]() 的面积要尽可能小,设
的面积要尽可能小,设![]() ,问:当
,问:当![]() 多大时
多大时![]() 的面积最小?最小面积是多少?
的面积最小?最小面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A. 命题![]() :
:![]() ,
,![]() ,则命题
,则命题![]() :
:![]() ,
,![]()
B. “![]() ”是“
”是“![]() ”的充要条件
”的充要条件
C. 命题“若![]() ,则
,则![]() 或
或![]() ”的逆否命题是“若
”的逆否命题是“若![]() 或
或![]() ,则
,则![]() ”
”
D. 命题![]() :
:![]() ,
,![]() ;命题
;命题![]() :对
:对![]() ,总有
,总有![]() ;则
;则![]() 是真命题
是真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在区间![]() 上的函数
上的函数![]() 的图象关于直线
的图象关于直线![]() 对称,当
对称,当![]() 时,函数
时,函数![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 的表达式;
的表达式;
(3)若关于![]() 的方程
的方程![]() 有解,那么将方程在
有解,那么将方程在![]() 取某一确定值时所求得的所有解的和记为
取某一确定值时所求得的所有解的和记为![]() ,求
,求![]() 的所有可能值及相应
的所有可能值及相应![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com