
【题目】已知F为抛物线E:![]() (p>0)的焦点,C(
(p>0)的焦点,C(![]() ,1)为E上一点,且|CF|=2.过F任作两条互相垂直的直线
,1)为E上一点,且|CF|=2.过F任作两条互相垂直的直线![]() ,
,![]() ,分别交抛物线E于P,Q和M,N两点,A,B分别为线段PQ和MN的中点.
,分别交抛物线E于P,Q和M,N两点,A,B分别为线段PQ和MN的中点.
(1)求抛物线E的方程及点C的坐标;
(2)试问![]() 是否为定值?若是,求出此定值;若不是,请说明理由;
是否为定值?若是,求出此定值;若不是,请说明理由;
(3)证明直线AB经过一个定点,求此定点的坐标,并求△AOB面积的最小值.
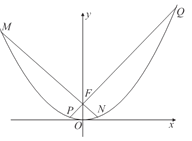
【答案】(1) 抛物线方程为![]() ,
,![]() 或
或![]() ;(2) 是定值,定值为
;(2) 是定值,定值为![]() ;(3) 过定点
;(3) 过定点![]() ;
;![]() 面积的最小值为6.
面积的最小值为6.
【解析】
![]() 根据抛物线的性质和定义即可求出
根据抛物线的性质和定义即可求出![]() ,代值计算即可求出点C的坐标,
,代值计算即可求出点C的坐标,
![]() 设直线
设直线![]() 的方程为
的方程为![]() ,
,![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() ,根据抛物线定义可得
,根据抛物线定义可得![]() ,
,![]() ,再分别联立方程组根据韦达定理可得
,再分别联立方程组根据韦达定理可得![]() ,
,![]() ,即可求出
,即可求出![]() ,
,
![]() 设
设![]() ,
,![]() ,由
,由![]() 分别求出点A,B的坐标,求出直线AB的斜率,写出直线方程,即可得到直线过定点
分别求出点A,B的坐标,求出直线AB的斜率,写出直线方程,即可得到直线过定点![]() ,再根据两点之间的距离公式和点到直线的距离公式可得表示三角形面积,根据基本不等式即可求出最值
,再根据两点之间的距离公式和点到直线的距离公式可得表示三角形面积,根据基本不等式即可求出最值
解:![]() 抛物线E:
抛物线E:![]() 的准线方程为
的准线方程为![]() ,
,
![]() 为E上一点,且
为E上一点,且![]() ,
,
![]() ,即
,即![]() ,
,
![]() 抛物线方程为
抛物线方程为![]() ,
,
当![]() 时,
时,![]() ,
,
即![]() 或
或![]() .
.
![]() 由
由![]() 可得
可得![]() ,
,
设直线![]() 的方程为
的方程为![]() ,
,![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
由![]() ,
,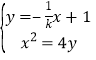 ,分别消x可得,
,分别消x可得,![]() ,
,![]() ,
,
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,
故![]() 是为定值,定值为
是为定值,定值为![]() .
.
![]() 设
设![]() ,
,![]() ,
,
![]() ,B分别为线段PQ和MN的中点,
,B分别为线段PQ和MN的中点,
![]() 由
由![]() 可得
可得![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
则直线AB的斜率为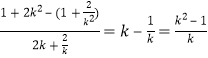 ,
,
![]() 直线AB的方程为
直线AB的方程为![]() ,即
,即![]() ,
,
![]() 直线AB过定点
直线AB过定点![]() ,
,
![]()
点![]() 到直线
到直线![]() 的距离
的距离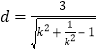 ,
,
![]() ,当且仅当
,当且仅当![]() 时取等号.
时取等号.
故![]() 面积的最小值为6.
面积的最小值为6.


科目:高中数学 来源: 题型:
【题目】[2018·临川一中]海盗船是一种绕水平轴往复摆动的游乐项目,因其外形仿照古代海盗船而得名.现有甲、乙两游乐场统计了一天6个时间点参与海盗船游玩的游客数量,具体数据如表:
时间点 | 8点 | 10点 | 12点 | 14点 | 16点 | 18点 |
甲游乐场 | 10 | 3 | 12 | 6 | 12 | 20 |
乙游乐场 | 13 | 4 | 3 | 2 | 6 | 19 |
(1)从所给6个时间点中任选一个,求参与海盗船游玩的游客数量甲游乐场比乙游乐场少的概率;
(2)记甲、乙两游乐场6个时间点参与海盗船游玩的游客数量分别为![]() ,
,![]() (
(![]() ),现从该6个时间点中任取2个,求恰有1个时间点满足
),现从该6个时间点中任取2个,求恰有1个时间点满足![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装店对过去100天其实体店和网店的销售量(单位:件)进行了统计,制成频率分布直方图如下:
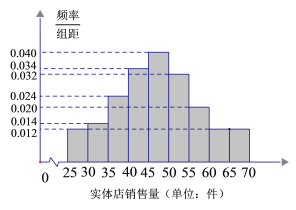
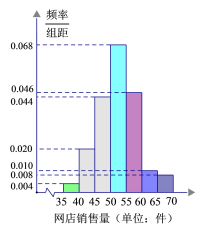
(1)若将上述频率视为概率,已知该服装店过去100天的销售中,实体店和网店销售量都不低于50件的概率为0.24,求过去100天的销售中,实体店和网店至少有一边销售量不低于50件的天数;
(2)若将上述频率视为概率,已知该服装店实体店每天的人工成本为500元,门市成本为1200元,每售出一件利润为50元,求该门市一天获利不低于800元的概率;
(3)根据销售量的频率分布直方图,求该服装店网店销售量中位数的估计值(精确到0.01).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A,B是R中两个子集,对于![]() ,定义:
,定义: 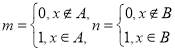 .①若
.①若![]() ;则对任意
;则对任意![]() ;②若对任意
;②若对任意![]() ,则
,则![]() ;③若对任意
;③若对任意![]() ,则A,B的关系为
,则A,B的关系为![]() .上述命题正确的序号是______. (请填写所有正确命题的序号)
.上述命题正确的序号是______. (请填写所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为庆祝成立二十周年,特举办《快乐大闯关》竞技类有奖活动,该活动共有四关,由两名男职员与两名女职员组成四人小组,设男职员闯过一至四关概率依次是![]() ,女职员闯过一至四关的概率依次是
,女职员闯过一至四关的概率依次是![]()
(1)求女职员闯过四关的概率;
(2)设![]() 表示四人小组闯过四关的人数,求随机变量
表示四人小组闯过四关的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】标号为0到9的10瓶矿泉水.
(1)从中取4瓶,恰有2瓶上的数字相邻的取法有多少种?
(2)把10个空矿泉水瓶挂成如下4列的形式,作为射击的靶子,规定每次只能射击每列最下面的一个(射中后这个空瓶会掉到地下),把10个矿泉水瓶全部击中有几种不同的射击方案?
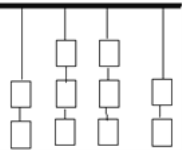
(3)把击中后的矿泉水瓶分送给A、B、C三名垃圾回收人员,每个瓶子1角钱.垃圾回收人员卖掉瓶子后有几种不同的收入结果?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《山东省高考改革试点方案》规定:从2017年秋季高中入学的新生开始,不分文理科;2020年开始,高考总成绩由语数外3门统考科目和物理、化学等六门选考科目构成.将每门选考科目的考生原始成绩从高到低划分为A、B+、B、C+、C、D+、D、E共8个等级.参照正态分布原则,确定各等级人数所占比例分别为3%、7%、16%、24%、24%、16%、7%、3%.选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到[91,100]、[81,90]、[71,80]、[61,70]、[51,60]、[41,50]、[31,40]、[21,30]八个分数区间,得到考生的等级成绩.
某校高一年级共2000人,为给高一学生合理选科提供依据,对六个选考科目进行测试,其中物理考试原始成绩基本服从正态分布N(60,169).
(Ⅰ)求物理原始成绩在区间(47,86)的人数;
(Ⅱ)按高考改革方案,若从全省考生中随机抽取3人,记X表示这3人中等级成绩在区间[61,80]的人数,求X的分布列和数学期望.
(附:若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() ,把圆
,把圆![]() 上每一点的横坐标伸长为原来的2倍,纵坐标不变,得到曲线
上每一点的横坐标伸长为原来的2倍,纵坐标不变,得到曲线![]() ,且倾斜角为
,且倾斜角为![]() ,经过点
,经过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)当![]() 时,求曲线
时,求曲线![]() 的普通方程与直线
的普通方程与直线![]() 的参数方程;
的参数方程;
(2)求点![]() 到
到![]() 两点的距离之积的最小值.
两点的距离之积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com