
【题目】已知圆![]() 经过点
经过点![]() ,圆
,圆![]() 的圆心在圆
的圆心在圆![]() 的内部,且直线
的内部,且直线![]() 被圆
被圆![]() 所截得的弦长为
所截得的弦长为![]() .点
.点![]() 为圆
为圆![]() 上异于
上异于![]() 的任意一点,直线
的任意一点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)求证: ![]() 为定值.
为定值.
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() 是
是![]() 上的点.
上的点.
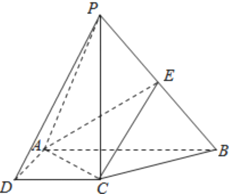
(1)求证: 平面![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,且二面角
的中点,且二面角![]() 的余弦值为
的余弦值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式组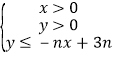 所表示的平面区域为
所表示的平面区域为![]() ,记
,记![]() 内的整点个数为
内的整点个数为![]() ,(整点即横、纵坐标均为整数的点)
,(整点即横、纵坐标均为整数的点)
(1)计算![]() 的值;
的值;
(2)求数列![]() 的通项公式
的通项公式![]() ;
;
(3)记数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,若对于一切的正整数
,若对于一切的正整数![]() ,总有
,总有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 在区间
在区间![]() 上,
上, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 均可为一个三角形的三边长,则称函数
均可为一个三角形的三边长,则称函数![]() 为“三角形函数”.已知函数
为“三角形函数”.已知函数![]() 在区间
在区间![]() 上是“三角形函数”,则实数
上是“三角形函数”,则实数![]() 的取值范围为( )
的取值范围为( )
A. 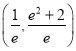 B.
B. ![]()
C. ![]() D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88,若样本B数据恰好是样本A数据都加上2后所得数据,则A,B两样本的下列数字特征对应相同的是( )
A. 众数 B. 平均数
C. 中位数 D. 标准差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() 过点
过点![]() .
.
(1)求圆![]() 的圆心坐标和半径;
的圆心坐标和半径;
(2)若直线![]() 与圆
与圆![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(3)若直线![]() 与圆
与圆![]() 相交于P,Q两点,求三角形CPQ的面积的最大值,并求此时
相交于P,Q两点,求三角形CPQ的面积的最大值,并求此时
直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的焦点在
的焦点在![]() 轴上.
轴上.
(1)若椭圆![]() 的焦距为1,求椭圆
的焦距为1,求椭圆![]() 的方程;
的方程;
(2)设![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为椭圆
为椭圆![]() 上第一象限内的点,直线
上第一象限内的点,直线![]() 交
交![]() 轴于点
轴于点![]() ,并且
,并且![]() .证明:当
.证明:当![]() 变化时,点
变化时,点![]() 在定直线
在定直线![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个铝合金窗分为上、下两栏,四周框架和中间隔档的材料为铝合金,宽均为6![]() ,上栏与下栏的框内高度(不含铝合金部分)的比为1:2,此铝合金窗占用的墙面面积为28800
,上栏与下栏的框内高度(不含铝合金部分)的比为1:2,此铝合金窗占用的墙面面积为28800![]() ,设该铝合金窗的宽和高分别为
,设该铝合金窗的宽和高分别为![]() ,铝合金窗的透光部分的面积为
,铝合金窗的透光部分的面积为![]() .
.

(1)试用![]() 表示
表示![]() ;
;
(2)若要使![]() 最大,则铝合金窗的宽和高分别为多少?
最大,则铝合金窗的宽和高分别为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com