
【题目】为考察高中生的性别与喜欢数学课程之间的关系,在某学校高中生中随机抽取了250名学生,得到如图的二维条形图.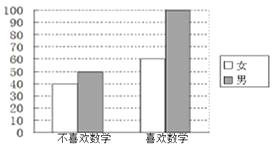
(1)根据二维条形图,完成下表:
男 | 女 | 合计 | |
喜欢数学课程 | |||
不喜欢数学课程 | |||
合计 |
(2)对照如表,利用列联表的独立性检验估计,请问有多大把握认为“性别与喜欢数学有关系”?
 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
【题目】某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员到篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:

(I)依据频率分布直方图估算该运动员投篮命中时,他到篮筐中心的水平距离的中位数;
(II)在某场比赛中,考察他前4次投篮命中时到篮筐中心的水平距离的情况,并且规定:运动员投篮命中时,他到篮筐中心的水平距离不少于4米的记1分,否则扣掉1分.用随机变量X表示第4次投篮后的总分,将频率视为概率,求X的分布列和均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2-lnx。
(Ⅰ)当a=![]() 时,判断f(x)的单调性;(Ⅱ)设f(x)≤x3+4x-lnx,在定义域内恒成立,求a的取值范围。
时,判断f(x)的单调性;(Ⅱ)设f(x)≤x3+4x-lnx,在定义域内恒成立,求a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有25周岁以上(含25周岁)工人300名,25周岁以 下工人200名.为研究工人的日平均生产量是否与年龄有关.现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“ 25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.

附表:
P( | 0.100 | 0 .010 | 0.001 |
k | 2.706 | 6.635 | 10.828 |
![]() ,(其中
,(其中 ![]() )
)
(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的频率.
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成 ![]() 的列联表,并判断是否有
的列联表,并判断是否有 ![]() 的把握认为“生产能手与工人所在的年龄组有关”?
的把握认为“生产能手与工人所在的年龄组有关”?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
已知直线l的参数方程为 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为![]() 。
。
(Ⅰ)求直线l以及曲线C的极坐标方程;
(Ⅱ)设直线l与曲线C交于A,B两点,求△PAB的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com