
【题目】设函数![]()
(I)求函数f(x)的单调区间;
(II)若![]() ,求证:
,求证:![]() 时,
时,![]() .
.
【答案】(I)当![]() 时,f(x)的单调减区间为
时,f(x)的单调减区间为![]() ;当
;当![]() 时,f(x)的单调减区间为
时,f(x)的单调减区间为![]() ,单调减区间为
,单调减区间为![]() (II)见详解
(II)见详解
【解析】
(I)采用分类讨论的方法,结合导数判断函数单调性,可得结果.
(II)构建新的函数,利用导数研究新函数的单调性,并求最小值,与0比较大小,可得结果.
解:(I)![]()
若![]() 时,则
时,则![]() ,
,
f(x)在![]() 上单调递减;
上单调递减;
若![]() 时,令
时,令![]() 解得:
解得:![]()
当![]() 时,
时,
则![]() ,f(x)单调递减;
,f(x)单调递减;
当![]() 时,
时,
则![]() ,f(x)单调递增;
,f(x)单调递增;
综上所述,
当![]() 时,f(x)的单调减区间为
时,f(x)的单调减区间为![]()
当![]() 时,f(x)的单调减区间为
时,f(x)的单调减区间为![]() ,
,
单调减区间为![]()
(II)当![]() 时,要证
时,要证![]() ,
,
即证![]() ,
,
亦即证![]()
令![]() ,则
,则![]()
由指数函数及幂函数的性质知:
![]() 在
在![]() 上是增函数
上是增函数
![]() ,
,![]() ,
,
![]() 在
在![]() 内存在唯一的零点,
内存在唯一的零点,
也即![]() 在
在![]() 上有唯一零点
上有唯一零点
设![]() 的零点为
的零点为![]() ,
,
则![]() ,即
,即![]() ,
,
由![]() 的单调性知:
的单调性知:
当![]() 时,
时,
![]() ,h(x)为减函数,
,h(x)为减函数,
当![]() 时,
时,
![]() ,h(x)为增函数,
,h(x)为增函数,
所以当![]() ,
,![]() 时,
时,
![]()
![]() ,即
,即![]() .
.


科目:高中数学 来源: 题型:
【题目】武汉市摄影协会准备在2020年1月举办主题为“我们都是追梦人”摄影图片展,通过平常人的镜头记录国强民富的幸福生活,摄影协会收到了来自社会各界的大量作品,打算从众多照片中选取100张照片展出,其参赛者年龄集中![]() 在之间,根据统计结果,做出频率分布直方图如图:
在之间,根据统计结果,做出频率分布直方图如图:

(1)求频率直方图中![]() 的值,并根据频率直方图,求这100位摄影者年龄的中位数;
的值,并根据频率直方图,求这100位摄影者年龄的中位数;
(2)为了展示不同年龄作者眼中的幸福生活,摄影协会按照分层抽样的方法,计划从这100件照片中抽出20个最佳作品,并邀请相应作者参加“讲述照片背后的故事”座谈会.
①在答题卡上的统计表中填出每组相应抽取的人数:
年龄 |
|
|
|
|
|
人数 |
②若从年龄在![]() 的作者中选出2人把这些图片和故事整理成册,求这2人中至少有1人的年龄在
的作者中选出2人把这些图片和故事整理成册,求这2人中至少有1人的年龄在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年圣诞节,各地的餐馆都出现了用餐需预定的现象,致使--些人在没有预定的情况下难以找到用餐的餐馆,针对这种现象,专家对人们“用餐地点"以及“性别”作出调查,得到的情况如下表所示:
在家用餐 | 在餐馆用餐 | 总计 | |
女性 |
| ||
男性 |
| ||
总计 |
|
|
(1)完成上述![]() 列联表;
列联表;
(2)根据表中的数据,试通过计算判断是否有![]() 的把握说明“用餐地点”与“性别"有关;
的把握说明“用餐地点”与“性别"有关;
(3)若在接受调查的所有人男性中按照“用餐地点”进行分层抽样,随机抽取![]() 人,再在
人,再在![]() 人中抽取
人中抽取![]() 人赠送餐馆用餐券,记收到餐馆用餐券的男性中在餐馆用餐的人数为
人赠送餐馆用餐券,记收到餐馆用餐券的男性中在餐馆用餐的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
|
|
|
|
|
|
|
|
![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线;
处的切线;
(2)若函数![]() 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,若在
,若在![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人们经济收入的不断增加,个人购买家庭轿车已不再是一种时尚,车的使用费用,尤其是随着使用年限的增多,所支出的费用到底会增长多少,一直是购车一族非常关心的问题,某汽车销售公司做了一次抽样调查,并统计得出2009年出售的某款车的使用年限![]() (2009年记
(2009年记![]() )与所支出的总费用
)与所支出的总费用![]() (万元)有如表的数据资料:
(万元)有如表的数据资料:
使用年限 | 2 | 3 | 4 | 5 | 6 |
总费用 | 2.5 | 3.5 | 5.5 | 6.5 | 7.0 |
(1)求线性回归方程![]() ;
;
(2)若这款车一直使用到2020年,估计使用该款车的总费用是多少元?
线性回归方程![]() 中斜率和截距用最小二乘法估计计算公式如下:
中斜率和截距用最小二乘法估计计算公式如下:
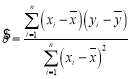
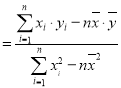 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() .
.
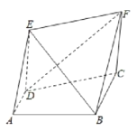
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出线段
,若存在,求出线段![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地种植常规稻![]() 和杂交稻
和杂交稻![]() ,常规稻
,常规稻![]() 的亩产稳定为485公斤,今年单价为3.70元/公斤,估计明年单价不变的可能性为
的亩产稳定为485公斤,今年单价为3.70元/公斤,估计明年单价不变的可能性为![]() ,变为3.90元/公斤的可能性为
,变为3.90元/公斤的可能性为![]() ,变为4.00的可能性为
,变为4.00的可能性为![]() .统计杂交稻
.统计杂交稻![]() 的亩产数据,得到亩产的频率分布直方图如图①.统计近10年杂交稻
的亩产数据,得到亩产的频率分布直方图如图①.统计近10年杂交稻![]() 的单价(单位:元/公斤)与种植亩数(单位:万亩)的关系,得到的10组数据记为
的单价(单位:元/公斤)与种植亩数(单位:万亩)的关系,得到的10组数据记为![]() ,并得到散点图如图②.
,并得到散点图如图②.
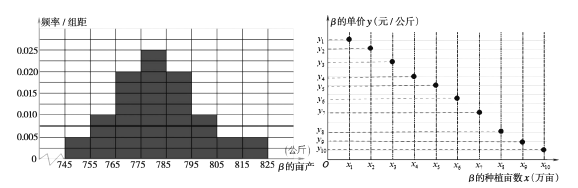
(1)根据以上数据估计明年常规稻![]() 的单价平均值;
的单价平均值;
(2)在频率分布直方图中,各组的取值按中间值来计算,求杂交稻![]() 的亩产平均值;以频率作为概率,预计将来三年中至少有二年,杂交稻
的亩产平均值;以频率作为概率,预计将来三年中至少有二年,杂交稻![]() 的亩产超过795公斤的概率;
的亩产超过795公斤的概率;
(3)①判断杂交稻![]() 的单价
的单价![]() (单位:元/公斤)与种植亩数
(单位:元/公斤)与种植亩数![]() (单位:万亩)是否线性相关?若相关,试根据以下的参考数据求出
(单位:万亩)是否线性相关?若相关,试根据以下的参考数据求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
②调查得知明年此地杂交稻![]() 的种植亩数预计为2万亩.若在常规稻
的种植亩数预计为2万亩.若在常规稻![]() 和杂交稻
和杂交稻![]() 中选择,明年种植哪种水稻收入更高?
中选择,明年种植哪种水稻收入更高?
统计参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
附:线性回归方程![]() ,
,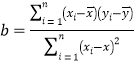 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com