
已知函数f(x)=2sinxcosx+cos2x(x∈R).
(1)求f(x)的最小正周期和最大值;
(2)若θ为锐角,且f(θ+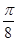 )=
)= ,求tan2θ的值.
,求tan2θ的值.
(1) f(x)的最小正周期为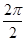 =π,最大值为.(2) tan2θ=
=π,最大值为.(2) tan2θ=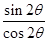 =2.
=2.
【解析】
试题分析:利用二倍角公式以及两角和的正弦函数化简函数为一个角的一个三角函数的形式,
(Ⅰ)直接利用周期公式求出函数f (x)的最小正周期,最大值易求.
(Ⅱ)由f(θ+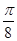 )=
)=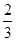 可得sin(2θ+
可得sin(2θ+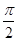 )=
)=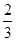 ,从而可得cos2θ=
,从而可得cos2θ=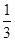 ,再注意研究0<2θ<π,进而可利用
,再注意研究0<2θ<π,进而可利用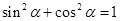 求出sin2θ,进而可求出tan2θ=
求出sin2θ,进而可求出tan2θ=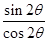 .
.
(1)f(x)=2sinxcosx+cos2x
=sin2x+cos2x
=(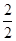 sin2x+
sin2x+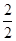 cos2x)
cos2x)
=sin(2x+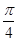 ).
).
∴f(x)的最小正周期为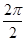 =π,最大值为.…………(6分)
=π,最大值为.…………(6分)
(2)∵f(θ+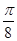 )=
)=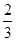 , ∴sin(2θ+
, ∴sin(2θ+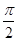 )=
)=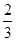 .
∴cos2θ=
.
∴cos2θ=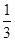 .
.
∵θ为锐角,即0<θ<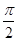 ,∴0<2θ<π.
,∴0<2θ<π.
∴sin2θ=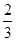 .
.
∴tan2θ=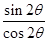 =2.…………(13分).
=2.…………(13分).
考点:倍角公式及两角和的正弦公式,正切公式,函数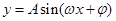 的性质,同角三角函数的基本关系式.
的性质,同角三角函数的基本关系式.
点评:本题主要是利用三角函数的二倍角公式,两角和的正弦公式,求解函数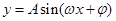 的最小正周期和最值,还考查了利用同角三角函数式求出其余名函数值,进而得到tan2θ的值.
的最小正周期和最值,还考查了利用同角三角函数式求出其余名函数值,进而得到tan2θ的值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:设计必修一数学北师版 北师版 题型:013
已知函数f(x)=2+log3x(1≤x≤9),则函数y=[f(x)]2+f(x2)的最大值为
A.6
B.13
C.22
D.33
查看答案和解析>>
科目:高中数学 来源:学习高手必修一数学苏教版 苏教版 题型:013
已知函数f(x)=2-x2,g(x)=x.若f(x)·g(x)=min{f(x),g(x)},那么f(x)·g(x)的最大值是
1
2
3
4
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 人教课标高一版(A必修1) 2009-2010学年 第7期 总163期 人教课标高一版 题型:044
已知函数f(x)=2(log2x)2+2alog2![]() +b,当x=
+b,当x=![]() 时,f(x)有最小值-8,求b的值.
时,f(x)有最小值-8,求b的值.
查看答案和解析>>
科目:高中数学 来源:湖北省孝感高级中学2011-2012学年高一上学期期中考试数学试题 题型:044
已知函数f(x)=2|x|-2.

(1)作出函数f(x)的图象;
(2)由图象指出函数的单调区间及单调性(不用证明);
(3)指出函数的值域.
查看答案和解析>>
科目:高中数学 来源:陕西省宝鸡市2010届高三教学质量检测(二)数学文科试题 题型:013
已知函数f(x)=(![]() )2-log2x,若实数x0是方程f(x)=0的解,且0<x1<x0,则f(x1)值的情况是
)2-log2x,若实数x0是方程f(x)=0的解,且0<x1<x0,则f(x1)值的情况是
恒为值负
等于0
恒为正值
不大于0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com