
【题目】如图,已知二面角α﹣MN﹣β的大小为60°,菱形ABCD在面β内,A、B两点在棱MN上,∠BAD=60°,E是AB的中点,DO⊥面α,垂足为O. 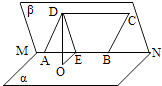
(1)证明:AB⊥平面ODE;
(2)求异面直线BC与OD所成角的余弦值.
【答案】
(1)证明:如图
∵DO⊥面α,ABα,∴DO⊥AB,
连接BD,由题设知,△ABD是正三角形,
又E是AB的中点,∴DE⊥AB,又DO∩DE=D,
∴AB⊥平面ODE;
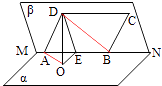
(2)解:∵BC∥AD,
∴BC与OD所成的角等于AD与OD所成的角,即∠ADO是BC与OD所成的角,
由(1)知,AB⊥平面ODE,
∴AB⊥OE,又DE⊥AB,于是∠DEO是二面角α﹣MN﹣β的平面角,
从而∠DEO=60°,不妨设AB=2,则AD=2,易知DE= ![]() ,
,
在Rt△DOE中,DO=DEsin60°= ![]() ,连AO,在Rt△AOD中,cos∠ADO=
,连AO,在Rt△AOD中,cos∠ADO= ![]() =
= ![]() ,
,
故异面直线BC与OD所成角的余弦值为 ![]() .
.
【解析】(1)运用直线与平面垂直的判定定理,即可证得,注意平面内的相交二直线;(2)根据异面直线的定义,找出所成的角为∠ADO,说明∠DEO是二面角α﹣MN﹣β的平面角,不妨设AB=2,从而求出OD的长,再在直角三角形AOD中,求出cos∠ADO.
【考点精析】解答此题的关键在于理解异面直线及其所成的角的相关知识,掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系,以及对直线与平面垂直的判定的理解,了解一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥的侧棱PD⊥底面ABCD,且底面ABCD是直角梯形,AD⊥CD,AB∥CD,AB=AD= ![]() CD=2,点M在侧棱上.
CD=2,点M在侧棱上.
(1)求证:BC⊥平面BDP;
(2)若侧棱PC与底面ABCD所成角的正切值为 ![]() ,点M为侧棱PC的中点,求异面直线BM与PA所成角的余弦值.
,点M为侧棱PC的中点,求异面直线BM与PA所成角的余弦值. 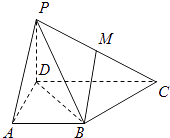
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(选修4﹣5:不等式选讲)
已知函数f(x)=|2x﹣1|+|2x+a|,g(x)=x+3.
(1)当a=﹣2时,求不等式f(x)<g(x)的解集;
(2)设a>﹣1,且当 ![]() 时,f(x)≤g(x),求a的取值范围.
时,f(x)≤g(x),求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对一批产品的长度(单位:毫米)进行抽样检测,如图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上为一等品,在区间[15,20)和[25,30)上为二等品,在区间[10,15)和[30,35]上为三等品.用频率估计概率,现从该批产品中随机抽取1件,则其为二等品的概率是( ) 
A.0.09
B.0.20
C.0.25
D.0.45
查看答案和解析>>
科目:高中数学 来源: 题型:
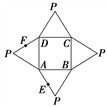
【题目】如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,
在此几何体中,给出下面四个结论:
①直线BE与直线CF异面; ②直线BE与直线AF异面;
③直线EF∥平面PBC; ④平面BCE⊥平面PAD.
其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
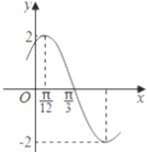
【题目】已知函数![]() 的部分图象如图所示.
的部分图象如图所示.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)将函数![]() 的图象做怎样的平移变换可以得到函数
的图象做怎样的平移变换可以得到函数![]() 的图象;
的图象;
(Ⅲ)若方程![]() 在
在![]() 上有两个不相等的实数根,求
上有两个不相等的实数根,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,E,F分别是A1B,A1C的中点,点D在B1C1上,A1D⊥B1C.求证: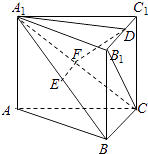
(1)EF∥平面ABC;
(2)平面A1FD⊥平面BB1C1C.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com