
![]()
(1)如果分别以t,α为参数,则所给的参数方程表示的图象分别是什么?请分别把它们转化为普通方程.(α为参数时,设t>0,t为参数时,设α≠![]() )
)
(2)求上述直线截上述曲线所得的弦长.
(3)根据上述求解过程总结出一个结论,并用基本语句编写一个算法计算弦长.
思路分析:本题综合考查参数方程,直线与曲线的位置关系以及算法等基本知识.首先根据参数方程的形式知:当t为参数时,参数方程表示直线,当α为参数表示圆,且直线恰好过圆的圆心,所以弦长就是圆的直径.根据所给的参数方程不难得到一般结论,用算法表示弦长只需根据数据求出圆的直径,所以只需使用顺序结构即可.
解:(1)以t为参数时,所给参数方程表示的图形是过点(2,5)且斜率为tanα的直线,化为普通方程是y-5=tanα(x-2);
以t为参数时,参数方程表示以(2,5)为圆心,半径为t的圆,化为普通方程是(x-2)2+(y-5)2=t2.
(2)上述直线恰好过圆的圆心,所以截圆所得弦长为圆的直径2t.
(3)根据上述计算过程可以总结出一般的结论为:对于一个参数方程
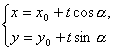 (α为参数时,设t>0,t为参数时,设α≠
(α为参数时,设t>0,t为参数时,设α≠![]() ),如果分别以t,α为参数,则所给的参数方程表示的图象分别是一条直线和一个圆,且直线过圆的圆心,所以直线截圆所得弦长是圆的直径2t.
),如果分别以t,α为参数,则所给的参数方程表示的图象分别是一条直线和一个圆,且直线过圆的圆心,所以直线截圆所得弦长是圆的直径2t.
用基本语句写出表示弦长的算法如下:
INPUT“参数t(t>0)”;t,
d=2t,
PRINT“所给参数方程表示的直线被圆截得的弦长是”;d,
END.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.请在答题纸指定区域内 作答.解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.请在答题纸指定区域内 作答.解答应写出文字说明、证明过程或演算步骤.
|
|
|
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省盐城中学高三(上)12月月考数学试卷(解析版) 题型:解答题
 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.请在答题纸指定区域内 作答.解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.请在答题纸指定区域内 作答.解答应写出文字说明、证明过程或演算步骤.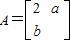 属于特征值-1的一个特征向量为
属于特征值-1的一个特征向量为 ,求矩阵A的逆矩阵.
,求矩阵A的逆矩阵. (t为参数,t∈{R}).试求曲线C上点M到直线l的距离的最大值.
(t为参数,t∈{R}).试求曲线C上点M到直线l的距离的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com