
(14分)如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知|AB|=3米,|AD|=2米,
(1)要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?
(2)当AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积.

(1)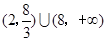 ;(2)SAMPN取得最小值24(平方米).
;(2)SAMPN取得最小值24(平方米).
【解析】设AN的长为x米(x>2),根据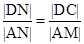 ,可求出|AM|=
,可求出|AM|=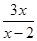
所以SAMPN=|AN|•|AM|=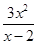 .
.
根据SAMPN > 32,解关于x的不等式即可.
从函数的角度求最值,可以求导,也可以变换成对号函数的形式利用均值不等式求最值
解:设AN的长为x米(x >2), ∵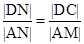 ,∴|AM|=
,∴|AM|=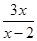
∴SAMPN=|AN|•|AM|=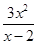
(1)由SAMPN
> 32 得 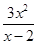 > 32
> 32
∵x >2,∴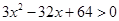 ,即(3x-8)(x-8)> 0
,即(3x-8)(x-8)> 0
∴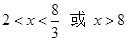 ,即AN长的取值范围是
,即AN长的取值范围是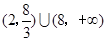 ……5分
……5分
(2)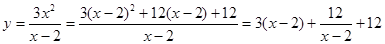
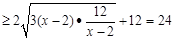
当且仅当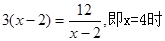 ,y=
,y=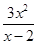 取得最小值.
取得最小值.
即SAMPN取得最小值24(平方米) ……………………10分


科目:高中数学 来源: 题型:
(08年安徽皖南八校联考)(本小题满分14分)
 如图所示,边长为2的等边△
如图所示,边长为2的等边△![]() 所在的平面垂直于矩形
所在的平面垂直于矩形![]() 所在的平面,
所在的平面,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)证明:![]() ⊥
⊥![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
 (本小题满分14分)
(本小题满分14分)
如图所示,在侧棱垂直于底面的三棱柱![]() 中,
中,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求四棱锥A-CBB1C1的体积;
(2)证明:![]()
![]() 平面
平面![]() ;
;
(3)若![]() 是棱
是棱![]() 的中点,在棱
的中点,在棱![]() 上是否存在一点
上是否存在一点![]() ,使
,使
![]() 平面
平面![]() ?证明你的结论.
?证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2015届湖南省高一上学期期末考试数学试卷(解析版) 题型:解答题
(本小题满分14分)
如图所示,在一个特定时段内,以点E为中心的10海里以内海域被设为警戒水域.点E正北40 海里处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东30°且与点A相距100海里的位置B,经过2小时又测得该船已行驶到点A北偏东60°且与点A相距20
海里处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东30°且与点A相距100海里的位置B,经过2小时又测得该船已行驶到点A北偏东60°且与点A相距20 海里的位置C.
海里的位置C.
(1)求该船的行驶速度(单位:海里/小时);
(2)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省湛江市高三8月第一次月考理科数学试卷(解析版) 题型:解答题
(本小题满分14分)如图所示,在四棱锥 中,
中, 平面
平面 ,
, ,
,
 ,
, ,
, 是
是 的中点.
的中点.
(1)证明: 平面
平面 ;
;
(2)若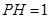 ,
, ,
, ,求二面角
,求二面角 的正切值.
的正切值.

查看答案和解析>>
科目:高中数学 来源:2012届浙江省宁波万里国际学校高三上期中理科数学试卷(解析版) 题型:解答题
(本题满分14分)如图所示,正方形 与矩形
与矩形 所在平面互相垂直,
所在平面互相垂直, ,点E为
,点E为 的中点.
的中点.

(Ⅰ)求证: ;
;
(Ⅱ)求证: ;
;
(III)在线段AB上是否存在点 ,使二面角
,使二面角 的大小为
的大小为 ?若存在,求出
?若存在,求出
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com