
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() 已知
已知![]()
![]()
(I)设![]() ,证明数列
,证明数列![]() 是等比数列;
是等比数列;
(II)求数列![]() 的通项公式.
的通项公式.![]()
【答案】(Ⅰ)见解析;(Ⅱ)![]()
【解析】此题主要考查了等比数列的性质及其前n项和,运用了错位相减法求数列{an}的前n项和,这个方法是高考中常用的方法,同学们要熟练掌握它
(Ⅰ)由题意只要证明bnbn-1
为一常数即可,已知Sn+1=4an+1,推出b1的值,然后继续递推相减,得an+1-2an=2(an-2an-1),从而求出bn与bn-1的关系;
(Ⅱ)根据(Ⅰ){bn}是等比数列,可得bn}的通项公式,从而证得数列{an![]() 2n }是首项为1
2n }是首项为1![]() 2 ,公差为1 2 的等差数列,最后利用错位相减法,求出数列{an}的通项公式
2 ,公差为1 2 的等差数列,最后利用错位相减法,求出数列{an}的通项公式
解:(I)由![]() 及
及![]() ,有
,有
![]()
![]()
由![]() ,...① 则当
,...① 则当![]() 时,有
时,有![]() .....②
.....②
②-①得![]()
又![]() ,
,![]()
![]() 是首项
是首项![]() ,公比为2的等比数列.
,公比为2的等比数列.
(II)由(I)可得![]() ,
,![]()
![]() 数列
数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列.
的等差数列.
![]()
![]() ,
,![]()


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】为了解某地参加2015 年夏令营的![]() 名学生的身体健康情况,将学生编号为
名学生的身体健康情况,将学生编号为![]() ,采用系统抽样的方法抽取一个容量为
,采用系统抽样的方法抽取一个容量为![]() 的样本,且抽到的最小号码为
的样本,且抽到的最小号码为![]() ,已知这
,已知这![]() 名学生分住在三个营区,从
名学生分住在三个营区,从![]() 到
到![]() 在第一营区,从
在第一营区,从![]() 到
到![]() 在第二营区,从
在第二营区,从![]() 到
到![]() 在第三营区,则第一、第二、第三营区被抽中的人数分别为( )
在第三营区,则第一、第二、第三营区被抽中的人数分别为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C经过点A(﹣2,0),B(0,2),且圆心C在直线y=x上,又直线l:y=kx+1与圆C相交于P、Q两点.
(1)求圆C的方程;
(2)若![]()
![]() =﹣2,求实数k的值;
=﹣2,求实数k的值;
(3)过点(0,4)作动直线m交圆C于E,F两点.试问:在以EF为直径的所有圆中,是否存在这样的圆P,使得圆P经过点M(2,0)?若存在,求出圆P的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在锐角△ABC中,两向量p=(2-2sin A,cos A+sin A),q=(sin A-cos A,1+sin A),且p与q是共线向量.
(1)求A的大小;
(2)求函数y=2sin2B+cos(![]() )取最大值时,角B的大小.
)取最大值时,角B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若有穷数列![]() (
(![]() 是正整数),满足
是正整数),满足![]() 即
即![]() (
(![]() 是正整数,且
是正整数,且![]() ),就称该数列为“对称数列”。例如,数列
),就称该数列为“对称数列”。例如,数列![]() 与数列
与数列![]() 都是“对称数列”.
都是“对称数列”.
(1)已知数列![]() 是项数为9的对称数列,且
是项数为9的对称数列,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列, ![]() ,
, ![]() ,试求
,试求![]() ,
, ![]() ,
, ![]() ,
, ![]() ,并求前9项和
,并求前9项和![]() .
.
(2)若![]() 是项数为
是项数为![]() 的对称数列,且
的对称数列,且![]() 构成首项为31,公差为
构成首项为31,公差为![]() 的等差数列,数列
的等差数列,数列![]() 前
前![]() 项和为
项和为![]() ,则当
,则当![]() 为何值时,
为何值时, ![]() 取到最大值?最大值为多少?
取到最大值?最大值为多少?
(3)设![]() 是
是![]() 项的“对称数列”,其中
项的“对称数列”,其中![]() 是首项为1,公比为2的等比数列.求
是首项为1,公比为2的等比数列.求![]() 前
前![]() 项的和
项的和![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点![]() 的椭圆
的椭圆![]() 经过点
经过点![]() ,且点
,且点![]() 为其右焦点.
为其右焦点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)是否存在平行于![]() 的直线
的直线![]() ,使得直线
,使得直线![]() 与椭圆
与椭圆![]() 有公共点,且直线
有公共点,且直线![]() 与
与![]() 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下:
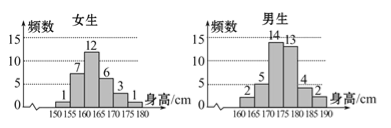
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185cm之间的概率;
(3)从样本中身高在180~190cm之间的男生中任选2人,求至少有1人身高在185~190cm之间的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com