
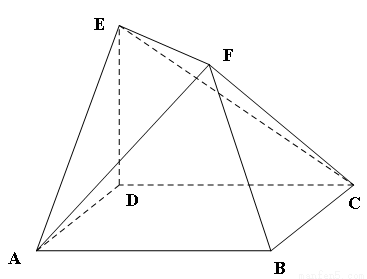
如图,ABCD是边长为2的正方形,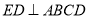 ,ED=1,
,ED=1,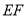 //BD,且
//BD,且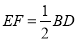 .
.
(1)求证:BF//平面ACE;
(2)求证:平面EAC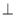 平面BDEF;
平面BDEF;
(3)求二面角B-AF-C的大小.
(1)证明见解析;(2)证明见解析;(3) .
.
【解析】
试题分析:(1)记 与
与 的交点为
的交点为 ,连接
,连接 ,则可证
,则可证 ,又
,又 面
面 ,
, 面
面 ,故
,故 平面
平面 ;
;
(2)因 ⊥平面
⊥平面 ,得
,得 ,又
,又 是正方形,所以
是正方形,所以 ,从而
,从而 平面
平面 ,又
,又
 面
面 ,故平面
,故平面
 平面
平面 ;
;
(3)过点 作
作 于点
于点 ,连接
,连接 ,则可证
,则可证 为二面角
为二面角 的平面角.在
的平面角.在 中,可求得
中,可求得 ,又
,又 ,故
,故 ,∴
,∴ ,即二面角
,即二面角 的大小为
的大小为 ;
;
证明:(1)记 与
与 的交点为
的交点为 ,连接
,连接 ,则
,则
所以 ,又
,又 ,所以
,所以
所以四边形 是平行四边形
是平行四边形
所以 ,
,
又 面
面 ,
, 面
面 ,
,
故 平面
平面 ;
;

(2)因 ⊥平面
⊥平面 ,所以
,所以 ,
,
又 是正方形,所以
是正方形,所以 ,
,
因为 面
面 ,
, 面
面 ,
,
所以 平面
平面 ,
,
又
 面
面 ,
,
故平面
 平面
平面 ;
;
(3)过点 作
作 于点
于点 ,连接
,连接 ,
,
因为 ,
, 面
面
所以 面
面 ,
,
因为 面
面 ,
,
所以
因为
所以 面
面
所以
又
所以 面
面
所以 ,即得
,即得 为二面角
为二面角 的平面角.
的平面角.
在 中,可求得
中,可求得 ,
,
又 ,故
,故 ,
,
∴ ,即二面角
,即二面角 的大小为
的大小为 ;
;
考点:线面平行的判定;面面垂直的判定;二面角的求解.


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源:2013-2014学年安徽省合肥市高三第二次教学质量检测理科数学试卷(解析版) 题型:选择题
已知正方体 中,线段
中,线段 上(不包括端点)各有一点
上(不包括端点)各有一点 ,且
,且 ,下列说法中,不正确的是( )
,下列说法中,不正确的是( )
 四点共面 B.直线
四点共面 B.直线 与平面
与平面 所成的角为定值
所成的角为定值
C. D.设二面角
D.设二面角 的大小为
的大小为 ,则
,则 的最小值为
的最小值为
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省“皖西七校”高三年级联合考试理科数学试卷(解析版) 题型:选择题
一个几何体按比例绘制的三视图如右图所示(单位: ),则该几何体的体积为( )
),则该几何体的体积为( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省“皖西七校”高三年级联合考试文科数学试卷(解析版) 题型:选择题
若直线 上不同的三个点
上不同的三个点 与直线
与直线 外一点
外一点 ,使得
,使得 成立,则满足条件的实数
成立,则满足条件的实数 的集合为( )
的集合为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省“江淮十校协作体”四月联考卷文科数学试卷(解析版) 题型:选择题
已知点P是圆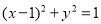 上异于坐标原点O的任意一点,直线OP的倾斜角为
上异于坐标原点O的任意一点,直线OP的倾斜角为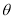 ,若
,若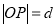 ,则函数
,则函数 的大致图像是 ( )
的大致图像是 ( )
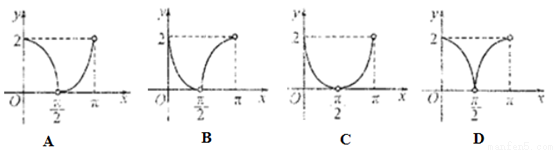
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市蓟县高三第一次模拟考试理科数学试卷(解析版) 题型:解答题
已知椭圆C的两个焦点分别为 ,且点
,且点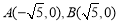 在椭圆C上,又
在椭圆C上,又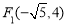 .
.
(1)求焦点F2的轨迹 的方程;
的方程;
(2)若直线 与曲线
与曲线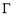 交于M、N两点,以MN为直径的圆经过原点,求实数b的取值范围.
交于M、N两点,以MN为直径的圆经过原点,求实数b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com