
【题目】已知单调递增的等比数列{an}满足a2+a3+a4=28,且a3+2是a2 , a4的等差中项.
(1)求数列{an}的通项公式;
(2)设bn=anlog2an , 其前n项和为Sn , 若(n﹣1)2≤m(Sn﹣n﹣1)对于n≥2恒成立,求实数m的取值范围.
【答案】
(1)解:设等比数列的{an}首项为a1,公比为q.
由题意可知: 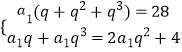 ,
,
解得: 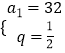 或
或 ![]() ,
,
∵数列为单调递增的等比数列,
∴an=2n;
(2)解:bn=anlog2an=n2n,
∴Sn=b1+b2+…+bn=121+222+…+n2n,①
2Sn=122+223+324+…+n2n+1,②
①﹣②,得:﹣Sn=2+22+23+…+2n﹣n2n+1
= ![]() ﹣n2n+1=2n+1﹣2﹣n2n+1,
﹣n2n+1=2n+1﹣2﹣n2n+1,
∴Sn=(n﹣1)2n+1+2,
若(n﹣1)2≤m(Sn﹣n﹣1)对于n≥2恒成立,
则(n﹣1)2≤m[(n﹣1)2n+1+2﹣n﹣1]=m[(n﹣1)2n+1+1﹣n]对于n≥2恒成立,
即 ![]() =
= ![]() 对于n≥2恒成立,
对于n≥2恒成立,
∵ ![]() =
= ![]() ,
,
∴数列{ ![]() }为递减数列,
}为递减数列,
则当n=2时, ![]() 的最大值为
的最大值为 ![]() .
.
∴m≥ ![]() .
.
则实数m得取值范围为[ ![]() ,+∞).
,+∞).
【解析】(1)设出等比数列{an}的首项和公比,由已知列式求得首项和公比,则数列{an}的通项公式可求;(2)把(1)中求得的通项公式代入bn=anlog2an , 利用错位相减法求得Sn , 代入(n﹣1)2≤m(Sn﹣n﹣1),分离变量m,由单调性求得最值得答案.
【考点精析】本题主要考查了对数的运算性质和数列的前n项和的相关知识点,需要掌握①加法:![]() ②减法:
②减法:![]() ③数乘:
③数乘:![]() ④
④![]() ⑤
⑤![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系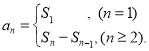 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】根据市场分析,某蔬菜加工点,当月产量为10吨至25吨时,月生产总成本![]() (万元)可以看出月产量
(万元)可以看出月产量![]() (吨)的二次函数,当月产量为10吨时,月生产成本为20万元,当月产量为15吨时,月生产总成本最低至17.5万元.
(吨)的二次函数,当月产量为10吨时,月生产成本为20万元,当月产量为15吨时,月生产总成本最低至17.5万元.
(I)写出月生产总成本![]() (万元)关于月产量
(万元)关于月产量![]() 吨的函数关系;
吨的函数关系;
(II)已知该产品销售价为每吨1.6万元,那么月产量为多少吨时,可获得最大利润,并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mex+x2+nx,{x|f(x)=0}={x|f(f(x))=0}≠,则m+n的取值范围为( )
A.(0,4)
B.[0,4)
C.[0,4]
D.(4,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
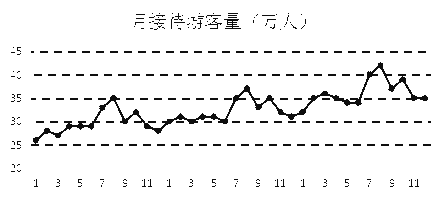
2014年 2015年 2016年
根据该折线图,下列结论错误的是( )
A. 年接待游客量逐年增加
B. 月接待游客量逐月增加
C. 各年的月接待游客量高峰期大致在7,8月
D. 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点C在椭圆M: ![]() =1(a>b>0)上,若点A(﹣a,0),B(0,
=1(a>b>0)上,若点A(﹣a,0),B(0, ![]() ),且
),且 ![]() =
= ![]()
![]() .
.
(1)求椭圆M的离心率;
(2)设椭圆M的焦距为4,P,Q是椭圆M上不同的两点.线段PQ的垂直平分线为直线l,且直线l不与y轴重合.
①若点P(﹣3,0),直线l过点(0,﹣ ![]() ),求直线l的方程;
),求直线l的方程;
②若直线l过点(0,﹣1),且与x轴的交点为D.求D点横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() 与常数
与常数![]() ,若
,若![]() 恒成立,则称
恒成立,则称![]() 为函数
为函数![]() 的一个“P数对”,设函数
的一个“P数对”,设函数![]() 的定义域为
的定义域为![]() ,且
,且![]() 。
。
(1)若![]() 是
是![]() 的一个“P数对”,且
的一个“P数对”,且![]() ,求常数
,求常数![]() 的值;
的值;
(2)若(1,1)是![]() 的一个“P数对”,且
的一个“P数对”,且![]() 在
在![]() 上单调递增,求函数
上单调递增,求函数![]() 在
在![]() 上的最大值与最小值;
上的最大值与最小值;
(3)若(-2,0)是![]() 的一个“P数对”,且当
的一个“P数对”,且当![]() 时,
时,![]() ,求k的值及
,求k的值及![]() 在区间
在区间![]() 上的最大值与最小值。
上的最大值与最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,C、D是以AB为直径的圆上两点,AB=2AD=2![]() ,AC=BC,F 是AB上一点,且AF=
,AC=BC,F 是AB上一点,且AF=![]() AB,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上,已知:
AB,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上,已知:![]() ,
, 
(1)求证:AD⊥平面BCE;
(2)求三棱锥A﹣CFD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com