
【题目】在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,![]() ,
,![]() ,
,
以AC的中点O为球心,AC为直径的球面交PD于点M,交PC于点N.

(1)求证:平面ABM⊥平面PCD;
(2)求直线CD与平面ACM所成角的大小;
(3)求点N到平面ACM的距离.
【答案】(1)证明见解析.
(2) ![]() .
.
(3) ![]() .
.
【解析】分析:(Ⅰ)要证平面ABM⊥平面PCD,只需证明平面PCD内的直线PD,垂直平面PAD内的两条相交直线BM、AB即可;(Ⅱ)先根据体积相等求出D到平面ACM的距离为h,即可求直线PC与平面ABM所成的角;(Ⅲ)先根据条件分析出所求距离等于点P到平面ACM距离的![]() ,设点P到平面ACM距离为h,再利用第二问的结论即可得到答案.
,设点P到平面ACM距离为h,再利用第二问的结论即可得到答案.
详解:
(1)AC是所作球面的直径,AM⊥MC,PA⊥平面ABCD,则PA⊥CD,又CD⊥AD,
∴CD⊥平面PAD,则CD⊥AM,∴AM⊥平面PCD,∴平面ABM⊥平面PCD;
(2)![]() ,
,![]() ,
,![]() ,设D到平面ACM的距离为h,
,设D到平面ACM的距离为h,
由![]() ,求得
,求得![]() ,∴
,∴![]() ,
,![]() ;
;
(3)![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,所求距离
,所求距离![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为( ) (参考数据: ![]() ≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)
≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)
A.12
B.24
C.36
D.48
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC= ![]() AD,∠BAD=∠ABC=90°,E是PD的中点.
AD,∠BAD=∠ABC=90°,E是PD的中点.
(Ⅰ)证明:直线CE∥平面PAB;
(Ⅱ)点M在棱PC 上,且直线BM与底面ABCD所成角为45°,求二面角M﹣AB﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是 ![]() 的中点.(12分)
的中点.(12分)
(Ⅰ)设P是 ![]() 上的一点,且AP⊥BE,求∠CBP的大小;
上的一点,且AP⊥BE,求∠CBP的大小;
(Ⅱ)当AB=3,AD=2时,求二面角E﹣AG﹣C的大小.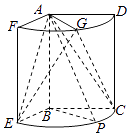
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在边长为1的正方体中,E,F,G,H分别为A1B1 , C1D1 , AB,CD的中点,点P从G出发,沿折线GBCH匀速运动,点Q从H出发,沿折线HDAG匀速运动,且点P与点Q运动的速度相等,记E,F,P,Q四点为顶点的三棱锥的体积为V,点P运动的路程为x,在0≤x≤2时,V与x的图象应为( )
A.
B.
C.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 的前
的前![]() 项和为
项和为![]() ,则下列命题:(1)若数列
,则下列命题:(1)若数列![]() 是递增数列,则数列
是递增数列,则数列![]() 也是递增数列;(2)数列
也是递增数列;(2)数列![]() 是递增数列的充要条件是数列
是递增数列的充要条件是数列![]() 的各项均为正数;(3)若
的各项均为正数;(3)若![]() 是等差数列(公差
是等差数列(公差![]() ),则
),则![]() 的充要条件是
的充要条件是![]() ;(4)若
;(4)若![]() 是等比数列,则
是等比数列,则![]() 的充要条件是
的充要条件是![]() .其中,正确命题的个数是( )
.其中,正确命题的个数是( )
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,an+1=an+n,利用如图所示的程序框图计算该数列的第10项,则判断框中应填的语句是( ) 
A.n>10
B.n≤10
C.n<9
D.n≤9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com