
分析 (Ⅰ)方程有两个不等实数根,从而判别式△>0,这样便可得出a<-1,或a>5,即得出了实数a的取值范围;
(Ⅱ)该方程有两个不等实数根,且这两个根都大于1,从而判别式△>0,由(Ⅰ)知a<-1,或a>5,并且小根满足大于1,即$\frac{2(1-a)-\sqrt{4(a-1)^{2}-4(2a+6)}}{2}>1$,解出该不等式,再根据a还需满足a<-1,或a>5即可得出实数a的取值范围;
(Ⅲ)先求f(x)的对称轴,x=1-a,讨论1-a和区间[-1,1]的关系:分1-a≤-1,-1<1-a≤0,0<1-a<1,和1-a≥1四种情况,在每种情况里,根据二次函数的单调性或取得顶点情况及端点值的比较,便可得出f(x)在[-1,1]上的最大值,和最小值,最后便可写出M(a),N(a).
解答 解:(Ⅰ)该方程有两个不等实数根;
∴△=4(a-1)2-4(2a+6)>0;
解得a<-1,或a>5;
(Ⅱ)该方程有两个不等实数根,根据(Ⅰ)便知,a<-1,或a>5;
且这两个根都大于1;
∴$\frac{2(1-a)-\sqrt{4(a-1)^{2}-4(2a+6)}}{2}>1$;
即$-2a>\sqrt{4({a}^{2}-4a-5)}$;
∴$-a>\sqrt{{a}^{2}-4a-5}$;
∴$\left\{\begin{array}{l}{a<0}\\{{a}^{2}>{a}^{2}-4a-5}\end{array}\right.$;
解得$-\frac{5}{4}<a<0$;
∴$-\frac{5}{4}<a<-1$;
∴实数a的取值范围为($-\frac{5}{4}$,-1);
(Ⅲ)f(x)的对称轴为x=1-a;
∴①1-a≤-1,即a≥2时,f(x)在[-1,1]上单调递增;
∴M(a)=f(1)=4a+5,N(a)=f(-1)=9;
②-1<1-a≤0,即1≤a<2时,M(a)=f(1)=4a+5,N(a)=f(1-a)=-a2+4a+5;
③0<1-a<1,即0<a<1时,M(a)=f(-1)=9,N(a)=f(1-a)=-a2+4a+5;
④1-a≥1,即a≤0时,f(x)在[-1,1]上单调递减;
∴M(a)=f(-1)=9,N(a)=f(1)=4a+5;
∴综上得,$M(a)=\left\{\begin{array}{l}{9}&{a<1}\\{4a+5}&{a≥1}\end{array}\right.$,$N(a)=\left\{\begin{array}{l}{4a+5}&{a≤0}\\{-{a}^{2}+4a+5}&{0<a<2}\\{9}&{a≥2}\end{array}\right.$.
点评 考查一元二次方程有两个不等实数根时判别式△的取值情况,一元二次方程的求根公式,二次函数的对称轴,以及根据二次函数的单调性或取得顶点情况,及对端点值的比较,从而得出函数最值的方法.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源: 题型:解答题
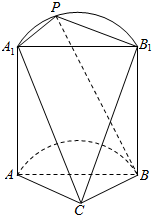 如图,这是一个半圆柱与多面体ABB1A1C构成的几何体,平面ABC与半圆柱的下底面共面,且AC⊥BC,P为$\widehat{{A}_{1}{B}_{1}}$上的动点.
如图,这是一个半圆柱与多面体ABB1A1C构成的几何体,平面ABC与半圆柱的下底面共面,且AC⊥BC,P为$\widehat{{A}_{1}{B}_{1}}$上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}+1}}{2}$ | B. | $\sqrt{3}+1$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\sqrt{5}-1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com