练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】2014年非洲爆发了埃博拉病毒疫情，在疫情结束后，当地防疫部门做了一项回访调查，得到如下结果，

    患病

    不患病

    有良好卫生习惯

    20

    180

    无良好卫生习惯

    80

    220

    （1）结合上面列联表，是否有的把握认为是否患病与卫生习惯有关？

    （2）现从有良好卫生习惯且不患病的180人中抽取，，，，共5人，再从这5人中选两人给市民做健康专题报告，求，至少有一人被选中的概率.

    0.050

    0.010

    0.001

    3.841

    6.635

    10.828

    【答案】（1）有99.9%的把握认为是否患病与卫生习惯有关（2）

    【解析】

    （1）首先将列联表补充完整，计算出的值，对照临界值得出结论；

    （2）用列举法求出基本事件数，计算所求的概率值.

    （1）

    患病

    不患病

    合计

    有良好卫生习惯

    20

    180

    200

    无良好卫生习惯

    80

    220

    300

    合计

    100

    400

    500

    有99.9%的把握认为是否患病与卫生习惯有关

    （2）从中任取2人，

    有共10种取法，

    其中仅有有三种：，

    其中仅有有三种：，

    有且有有一种：，

    故至少一人取到的概率

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

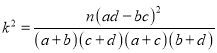
    科目：高中数学 来源： 题型：

    【题目】已知，如图四棱锥中，底面为菱形，，，平面，E，M分别是BC，PD中点，点F在棱PC上移动.

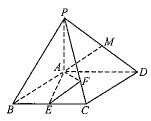
    （1）证明无论点F在PC上如何移动，都有平面平面；

    （2）当直线AF与平面PCD所成的角最大时，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数集，其中，且，若对，与两数中至少有一个属于，则称数集具有性质.

    （1）分别判断数集与数集是否具有性质，说明理由；

    （2）已知数集具有性质，判断数列，，…，是否为等差数列，若是等差数列，请证明；若不是，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】点F2是双曲线的右焦点，动点A在双曲线左支上，直线l1：tx﹣y+t﹣2＝0与直线l2：x+ty+2t﹣1＝0的交点为B，则|AB|+|AF2|的最小值为（ ）

    A.8B.C.9D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在党中央的英明领导下，在全国人民的坚定支持下，中国的抗击“新型冠状肺炎”战役取得了阶段性胜利，现在摆在我们大家面前的是有序且安全的复工复产.某商场为了提振顾客的消费信心，对某中型商品实行分期付款方式销售，根据以往资料统计，顾客购买该商品选择分期付款的期数ξ的分布列为

    其中0＜a＜1，0＜b＜1.

    （1）求购买该商品的3位顾客中，恰有1位选择分4期付款的概率；

    （2）商场销售一件该商品，若顾客选择分4期付款，则商场获得的利润为2000元；若顾客选择分5期付款，则商场获得的利润为2500元；若顾客选择分6期付款，则商场获得的利润为3000元，假设该商场销售两件该商品所获得的利润为X（单位：元），

    （i）设X＝5500时的概率为m，求当m取最大值时，利润X的分布列和数学期望；

    （ii）设某数列{xn}满足x1＝0.4，xn＝a，2xn+1＝b，若a＜0.25，求n的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

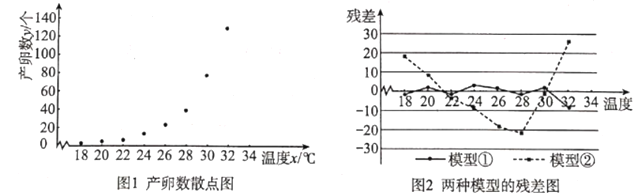
    【题目】红铃虫（Pectinophora gossypiella）是棉花的主要害虫之一，其产卵数与温度有关.现收集到一只红铃虫的产卵数y（个）和温度x（℃）的8组观测数据，制成图1所示的散点图.现用两种模型①，②分别进行拟合，由此得到相应的回归方程并进行残差分析，进一步得到图2所示的残差图.

    根据收集到的数据，计算得到如下值：

    25

    2.89

    646

    168

    422688

    48.48

    70308

    表中；；；；

    （1）根据残差图，比较模型①、②的拟合效果，应选择哪个模型？并说明理由；

    （2）根据（1）中所选择的模型，求出y关于x的回归方程（系数精确到0.01），并求温度为34℃时，产卵数y的预报值.

    （参考数据：，，，）

    附：对于一组数据，，…，，其回归直线的斜率和截距的最小二乘估计分别为，.

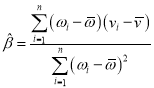    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C：＋＝1(a>b>0)的两焦点之间的距离为2，两条准线间的距离为8，直线l：y＝k(x－m)(m∈R)与椭圆交于P，Q两点．

    (1) 求椭圆C的方程；

    (2) 设椭圆的左顶点为A，记直线AP，AQ的斜率分别为k1，k2.①若m＝0，求k1k2的值；②若k1k2＝－，求实数m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某班级共有50名同学（男女各占一半），为弘扬传统文化，班委组织了“古诗词男女对抗赛”，将同学随机分成25组，每组男女同学各一名，每名同学均回答同样的五个不同问题，答对一题得一分，答错或不答得零分，总分5分为满分.最后25组同学得分如下表：

    组别号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    13

    男同学得分

    5

    4

    5

    5

    4

    5

    5

    4

    4

    4

    5

    5

    4

    女同学得分

    4

    3

    4

    5

    5

    5

    4

    5

    5

    5

    5

    3

    5

    分差

    1

    1

    1

    0

    -1

    0

    1

    -1

    -1

    -1

    0

    2

    -1

    组别号

    14

    15

    16

    17

    18

    19

    20

    21

    22

    23

    24

    25

    男同学得分

    4

    3

    4

    4

    4

    4

    5

    5

    5

    4

    3

    3

    女同学得分

    5

    3

    4

    5

    4

    3

    5

    5

    3

    4

    5

    5

    分差

    -1

    0

    0

    -1

    0

    1

    0

    0

    2

    0

    -2

    -2

    （I）完成列联表，并判断是否有90%的把握认为“该次对抗赛是否得满分”与“同学性别”有关；

    （Ⅱ）某课题研究小组假设各组男女同学分差服从正态分布，首先根据前20组男女同学的分差确定和，然后根据后面5组同学的分差来检验模型，检验方法是：记后面5组男女同学分差与的差的绝对值分别为，若出现下列两种情况之一，则不接受该模型，否则接受该模型.①存在；②记满足的i的个数为k，在服从正态分布的总体（个体数无穷大）中任意取5个个体，其中落在区间内的个体数大于或等于k的概率为P，.

    试问该课题研究小组是否会接受该模型.

    0.10

    0.05

    0.010

    2.706

    3.841

    6.635

    参考公式和数据：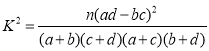

    ，；若，有，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】很多关于整数规律的猜想都通俗易懂，吸引了大量的数学家和数学爱好者，有些猜想已经被数学家证明，如“费马大定理”，但大多猜想还未被证明，如“哥德巴赫猜想”、“角谷猜想”.“角谷猜想”的内容是：对于每一个正整数，如果它是奇数，则将它乘以再加1；如果它是偶数，则将它除以；如此循环，最终都能够得到.下图为研究“角谷猜想”的一个程序框图.若输入的值为，则输出i的值为（ ）

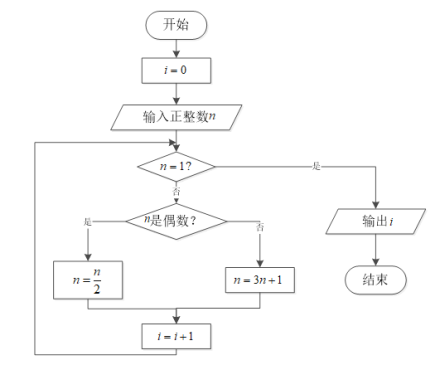
    A.B.C.D.

    查看答案和解析>>

    同步练习册答案