
【题目】如图,在三棱锥![]() 中,
中,![]() ,
,![]() 是以
是以![]() 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点.
的中点.
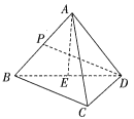
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析
(2)![]()
【解析】
(1)先在![]() 中运用等边三角形的性质得
中运用等边三角形的性质得![]() ,再在
,再在![]() 中利用勾股定理的逆定理得
中利用勾股定理的逆定理得![]() ,最后利用线面垂直的判定定理证明即可;
,最后利用线面垂直的判定定理证明即可;
(2)以![]() 所在的直线为
所在的直线为![]() 轴建立如图所示的空间直角坐标系,求得平面
轴建立如图所示的空间直角坐标系,求得平面![]() 的一个法向量,利用向量的夹角公式,即可求解.
的一个法向量,利用向量的夹角公式,即可求解.
(1)由题意,![]() 是边长为2的等边三角形,
是边长为2的等边三角形,
因为![]() 为
为![]() 的中点,所以
的中点,所以![]() ,且
,且![]() .
.
如图(1)所示,连接![]() ,因为
,因为![]() 是斜边长为2的等腰直角三角形,所以
是斜边长为2的等腰直角三角形,所以![]() .
.
在![]() 中,
中,![]() ,可得
,可得![]() ,所以
,所以![]() ,
,
又因为![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)由(1)可知![]() 平面
平面![]() ,且
,且![]() ,
,
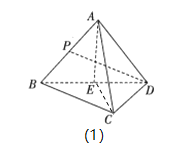
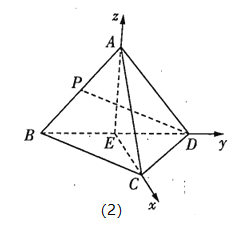
分别以![]() 所在的直线为
所在的直线为![]() 轴建立如图(2)所示的空间直角坐标系,
轴建立如图(2)所示的空间直角坐标系,
则![]() ,
,![]() ,
,
可得![]() ,
,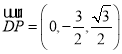 ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则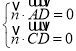 ,即
,即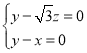 ,
,
取![]() ,则
,则![]() ,所以
,所以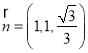 为平面
为平面![]() 的一个法向量,
的一个法向量,
设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则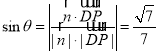 ,
,
故直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线C的参数方程为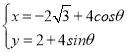 (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为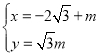 (m为参数),以平面直角坐标系的原点O为极点,x轴正半轴为极轴,建立坐标系.
(m为参数),以平面直角坐标系的原点O为极点,x轴正半轴为极轴,建立坐标系.
(1)求曲线C的极坐标方程;
(2)直线l与曲线C相交于M,N两点,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从2020年起,北京考生的高考成绩由语文、数学、外语3门统一高考成绩和考生选考的3门普通高中学业水平考试等级性考试科目成绩构成.等级性考试成绩位次由高到低分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,各等级人数所占比例依次为:
,各等级人数所占比例依次为:![]() 等级15%,
等级15%,![]() 等级40%,
等级40%,![]() 等级30%,
等级30%,![]() 等级14%,
等级14%,![]() 等级1%.现采用分层抽样的方法,从参加历史等级性考试的学生中抽取1000人作为样本,则该样本中获得
等级1%.现采用分层抽样的方法,从参加历史等级性考试的学生中抽取1000人作为样本,则该样本中获得![]() 或
或![]() 等级的学生人数为( )
等级的学生人数为( )
A.275B.400C.550D.450
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新型冠状病毒肺炎是一种急性感染性肺炎,其病原体是一种先前未在人类中发现的新型冠状病毒,即2019新型冠状病毒.2020年2月7日,国家卫健委决定将“新型冠状病毒感染的肺炎”暂命名为“新型冠状病毒肺炎”,简称“新冠肺炎”.患者初始症状多为发热、乏力和干咳,并逐渐出现呼吸困难等严重表现.基于目前流行病学调查,潜伏期为1~14天,潜伏期具有传染性,无症状感染者也可能成为传染源.某市为了增强民众防控病毒的意识,举行了“预防新冠病毒知识竞赛”网上答题,随机抽取![]() 人,答题成绩统计如图所示.
人,答题成绩统计如图所示.
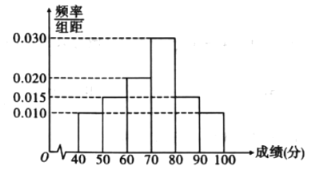
(1)由直方图可认为答题者的成绩![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 分别为答题者的平均成绩
分别为答题者的平均成绩![]() 和成绩的方差
和成绩的方差![]() ,那么这
,那么这![]() 名答题者成绩超过
名答题者成绩超过![]() 分的人数估计有多少人?(同一组中的数据用该组的区间中点值作代表)
分的人数估计有多少人?(同一组中的数据用该组的区间中点值作代表)
(2)如果成绩超过![]() 分的民众我们认为是“防御知识合格者”,用这
分的民众我们认为是“防御知识合格者”,用这![]() 名答题者的成绩来估计全市的民众,现从全市中随机抽取
名答题者的成绩来估计全市的民众,现从全市中随机抽取![]() 人,“防御知识合格者”的人数为
人,“防御知识合格者”的人数为![]() ,求
,求![]() .(精确到
.(精确到![]() )
)
附:①![]() ,
,![]() ;②
;②![]() ,则
,则![]() ,
,![]() ;③
;③![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数![]() (其中
(其中![]() )的图象如图所示,为了得到
)的图象如图所示,为了得到![]() 的图象,则只要将
的图象,则只要将![]() 的图象上所有的点( )
的图象上所有的点( )

A.向左平移![]() 个单位长度,纵坐标缩短到原来的
个单位长度,纵坐标缩短到原来的![]() ,横坐标不变
,横坐标不变
B.向左平移![]() 个单位长度,纵坐标伸长到原来的3倍横坐标不变
个单位长度,纵坐标伸长到原来的3倍横坐标不变
C.向右平移![]() 个单位长度,纵坐标缩短到原来的
个单位长度,纵坐标缩短到原来的![]() ,横坐标不变
,横坐标不变
D.向右平移![]() 个单位长度,纵坐标伸长到原来的3倍,横坐标不变
个单位长度,纵坐标伸长到原来的3倍,横坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).以原点
).以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)若直线![]() 与圆
与圆![]() 有公共点,试求实数
有公共点,试求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,过点
时,过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 交圆
交圆![]() 于
于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() 是关于
是关于![]() 的方程
的方程![]() 的两个不等的实根,且
的两个不等的实根,且![]() ,函数
,函数![]() 的定义域为
的定义域为![]() ,记
,记![]() ,
,![]() 分别为函数
分别为函数![]() 的最大值和最小值.
的最大值和最小值.
(1)试判断![]() 在
在![]() 上的单调性;
上的单调性;
(2)设![]() ,若函数
,若函数![]() 是奇函数,求实数
是奇函数,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】福利彩票“双色球”中红色球由编号为![]() 的
的![]() 个球组成.某彩民利用下面的随机数表选取
个球组成.某彩民利用下面的随机数表选取![]() 组数作为
组数作为![]() 个红色球的编号,选取方法是从随机数表(如下)第
个红色球的编号,选取方法是从随机数表(如下)第![]() 行的第
行的第![]() 列数字开始从左向右依次选取两个数字,则选出来的第
列数字开始从左向右依次选取两个数字,则选出来的第![]() 个红色球的编号为( )
个红色球的编号为( )
49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 17 34 91 64 |
57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 |
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com