
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)设![]() ,其中
,其中![]() 为函数
为函数![]() 的导函数.判断
的导函数.判断![]() 在定义域内是否为单调函数,并说明理由.
在定义域内是否为单调函数,并说明理由.
【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1) ![]() ,对a分类讨论,得到函数
,对a分类讨论,得到函数![]() 的单调区间;(2)
的单调区间;(2)![]() ,记
,记![]() ,则函数
,则函数![]() 为开口向上的二次函数.方程
为开口向上的二次函数.方程![]() 的判别式
的判别式![]() 恒成立.所以,
恒成立.所以, ![]() 有正有负. 从而
有正有负. 从而![]() 有正有负.
有正有负. ![]() 在定义域内不为单调函数.
在定义域内不为单调函数.
试题解析:
(Ⅰ)函数![]() 的定义域为
的定义域为![]() .
.![]() .
.
当![]() 时,令
时,令![]() ,解得:
,解得: ![]() 或
或![]() ,
, ![]() 为减函数;
为减函数;
令![]() ,解得:
,解得: ![]() ,
, ![]() 为增函数.
为增函数.
当![]() 时,
时, ![]() 恒成立,函数
恒成立,函数![]() 为减函数;
为减函数;
当![]() 时,令
时,令![]() ,解得:
,解得: ![]() 或
或![]() ,函数
,函数![]() 为减函数;
为减函数;
令![]() ,解得:
,解得: ![]() ,函数
,函数![]() 为增函数.
为增函数.
综上,
当![]() 时,
时, ![]() 的单调递减区间为
的单调递减区间为![]() ;单调递增区间为
;单调递增区间为![]() ;
;
当![]() 时,
时, ![]() 的单调递减区间为
的单调递减区间为![]() ;
;
当![]() 时,
时, ![]() 的单调递减区间为
的单调递减区间为![]() ;单调递增区间为
;单调递增区间为![]() .
.
(Ⅱ)![]() 在定义域内不为单调函数,以下说明:
在定义域内不为单调函数,以下说明:
![]() .
.
记![]() ,则函数
,则函数![]() 为开口向上的二次函数.
为开口向上的二次函数.
方程![]() 的判别式
的判别式![]() 恒成立.
恒成立.
所以, ![]() 有正有负. 从而
有正有负. 从而![]() 有正有负.
有正有负.
故![]() 在定义域内不为单调函数.
在定义域内不为单调函数.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
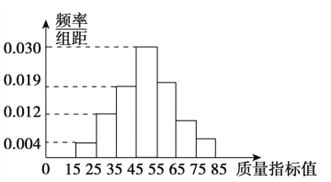
【题目】质检部门从企业生产的产品中抽取100件,测量这些产品的质量指标值,由测量结果得到如图的频率分布直方图,质量指标值落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.
(Ⅰ)求这些产品质量指标值落在区间![]() 内的频率;
内的频率;
(Ⅱ)若将频率视为概率,从该企业生产的这种产品中随机抽取3件,记这3件产品中质量指标值位于区间![]() 内的产品件数为
内的产品件数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=1﹣nan(n∈N*)
(1)计算a1 , a2 , a3 , a4;
(2)猜想an的表达式,并用数学归纳法证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 的图象过点(0,﹣1).
的图象过点(0,﹣1).
(1)求实数a的值;
(2)若f(x)=m+ ![]() (m,n是常数),求实数m,n的值;
(m,n是常数),求实数m,n的值;
(3)用定义法证明:函数f(x)在(3,+∞)上是单调减函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为[﹣1,5],部分对应值如表,
x | ﹣1 | 0 | 4 |
f(x) | 1 | 2 | 2 |
f(x)的导函数y=f′(x)的图象(该图象关于(2,0)中心对称) 如图所示.
下列关于f(x)的命题:
①函数f(x)的极大值点为 0与4;
②函数f(x)在[0,2]上是减函数;
③函数y=f(x)﹣a零点的个数可能为0、1、2、3、4个;
④如果当时x∈[﹣1,t],f(x)的最大值是2,那么t的最大值为5;.
⑤函数f(x)的图象在a=1是上凸的
其中一定正确命题的序号是 . 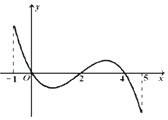
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一台机器按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,具有线性相关关系,下表为抽样试验的结果:
转速x(转/秒) | 8 | 10 | 12 | 14 | 16 |
每小时生产有缺点的零件数y(件) | 5 | 7 | 8 | 9 | 11 |
参考公式: ![]() ,
, ![]() =
= 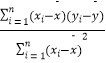 =
= 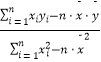 .
.
(1)如果y对x有线性相关关系,求回归方程;
(2)若实际生产中,允许每小时生产的产品中有缺点的零件最多有10个,那么机器的运转速度应控制在设么范围内?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com