解:(1)取AC的中点M,因为AB=AC,所以BM⊥AC
∵平面ABC⊥平面ACD,∴BM⊥平面ACD,∴BM⊥CD
∵AB=BC=CD=a,∠B=

∴∠BAC=∠BCA=

∵∠ACD=

,∴∠ACD=

,即AC⊥CD
∵AC∩BM=M∴CD⊥平面ABC∴CD⊥AB
∵AB⊥BC且BC∩CD=C
AB⊥平面BCD
(2)由(1)知BA为B到平面ACD的距离,且BM=
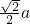
设点C到平面ABD的距离h
由已知可得AC=

,∠ACD=

,由(1)可得∠AMD=

,从而可得
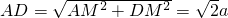
根据等体积可得

×
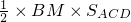
=
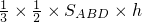
∴
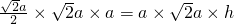
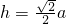
点C到平面ABD的距离
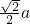
(3)假设存在满足条件的P,使得CP⊥平面ABD
则CP⊥BD①,∵BC=CD=a∴P为DB的中点
而此时CP=

,AP=
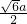
,AC=

,则AC
2=AP
2+CP
2∴AP⊥CP②由①②根据直线与平面垂直的判定定理可得此时的P满足条件,
故存在P为BD的中点
分析:(1)由AB=AC考虑取AC的中点M,则有BM⊥AC,由已知平面ABC⊥平面ACD可得BM⊥平面ACD进而有BM⊥CD,结合直线与平面垂直的判定定理可证
(2)利用等体积,根据V
B-ACD=V
C-ABD,代入已知数据可求点C到平面ABD的距离
(3)假设存在满足条件的P,使得CP⊥平面ABD则CP⊥BD,由BC=CD=a 可得P为DB的中点,从而通过计算可得AP⊥CP,根据直线与平面垂直的判定定理可得存在符合条件的点P
点评:本题体主要考查了“线线垂直”与“线面垂直”的相互转化,其理论依据是直线与平面垂直的判定定理与性质定理,而利用换顶点求三棱锥的体积进而求高是在求解点到面的距离时常用的方法.

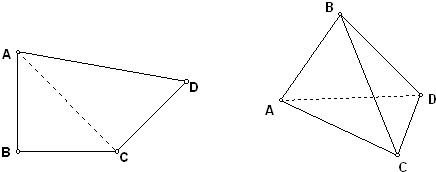 如图,平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠C=135°,沿对角线AC将△ABC折起,使平面ABC与平面ACD互相垂直.
如图,平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠C=135°,沿对角线AC将△ABC折起,使平面ABC与平面ACD互相垂直. ∴∠BAC=∠BCA=
∴∠BAC=∠BCA=
 ,∴∠ACD=
,∴∠ACD= ,即AC⊥CD
,即AC⊥CD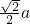
 ,∠ACD=
,∠ACD= ,由(1)可得∠AMD=
,由(1)可得∠AMD= ,从而可得
,从而可得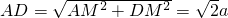
 ×
×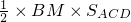 =
=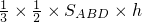
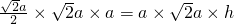
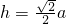
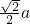
 ,AP=
,AP=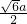 ,AC=
,AC= ,则AC2=AP2+CP2
,则AC2=AP2+CP2

 如图,平面四边形ABCD中,AB=AD=CD=1,BD=
如图,平面四边形ABCD中,AB=AD=CD=1,BD= 如图,平面四边形ABCD中,AB=AD=CD=1,BD=
如图,平面四边形ABCD中,AB=AD=CD=1,BD= 如图,平面四边形ABCD中,AB=13,AC=10,AD=5,cos∠DAC=
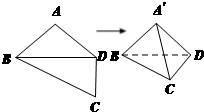
如图,平面四边形ABCD中,AB=13,AC=10,AD=5,cos∠DAC= 如图:平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠BCD=135°,沿对角线AC将△ADC折起,使面ADC⊥面ABC,
如图:平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠BCD=135°,沿对角线AC将△ADC折起,使面ADC⊥面ABC,